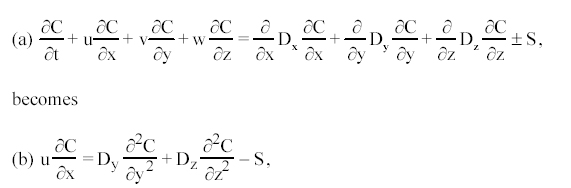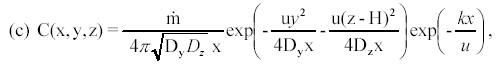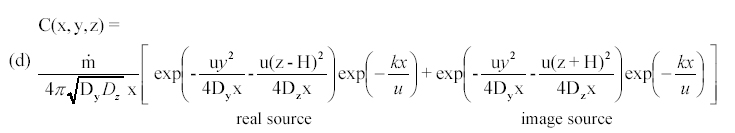Solution to Problem 9.1
For a continuously operating
smokestack and steady climatic conditions, we can assume a steady
concentration field, i.e. 
C/t
= 0. The wind is given as u = 5 m/s, implying v = w = 0. We are
told to assume a uniform wind, i.e. no shear, so we neglect shear-dispersion.
For the length-scale
of interest, Lx = 10,000m, the Peclet number
is (5m/s)(10,000m)/(1m2/s)
= 50,000 >>> 1. With
this high value of Pe, the longitudinal diffusion term is negligible relative
to longitudinal
advection, and we drop it. With the above assumptions, the transport equation
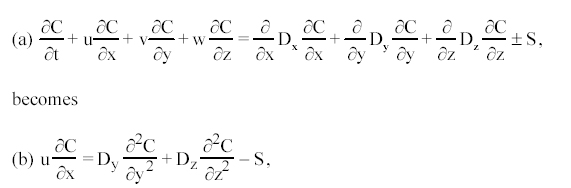
with S = 0 for Freon
and S = kTCEC for the TCE.
For a continuous release,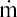 
= 5 kg/min = 83 g/s at (x,y,z) = (0, 0, H), the solution to (b) is
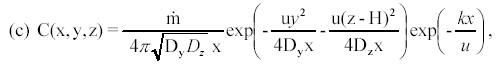
where k = 0 for Freon
and k = kTCE for the TCE. To account for the
no-flux boundary we add a
positive image source at (x,y,z) = (0, 0, -H).
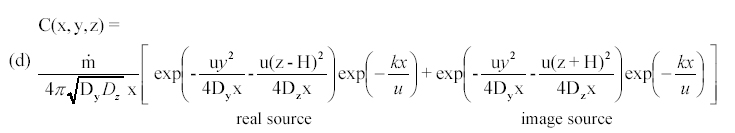
In any transverse dimension
for which the plume is unbounded (here the y-direction), the
maximum concentration is at the centerline of the plume (here y = 0). The vertical
coordinate,
however, is bounded by a no-flux boundary at the ground, z = 0. Once the plume
reaches the
ground, concentration will build up at the no-flux boundary. Because the upper
edge of the
plume is not bounded, the vertical concentration field will eventually become
asymmetric with
the maximum concentration at the ground. We estimate the distance at which this
will occur
using the time-scale for the edge of the plume (the 2
contour) to reach the ground,
(e) T,2=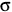
H2/(8Dz) =
(20m)2 / (8 x 0.1 m2s-1)
= 500 s.
Thus, for x >>
(u T,2)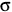
= 2500 m, which includes the point of interest, we expect the maximum
concentration to be at the ground. Therefore, the maximum concentration at x
= 10,000 m will
be Cmax = C (x =10000 m , y = 0, z = 0). Evaluating
(d) for Freon and TCE we find,
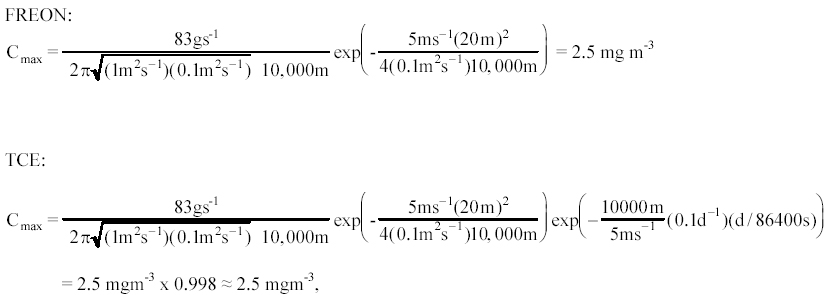
Very little degradation of TCE occurs over the 10,000m distance.
Close window and return to problem