Conceptual Model for Diffusion
Diffusion is defined as the net
transport due to random motion. A
model for diffusive flux can be constructed from the following simple example. Consider a one-dimensional system with motion
in the X direction only. An interface B-B' separates two regions
of different concentration, C1 and
C2 = particles/volume on the left
and right side of the interface, respectively.
The motion of each particle is a one-dimensional random walk. In each time interval,
x, each particle will move a distance 
x, moving right (+x) or left (-x) with equal probability.
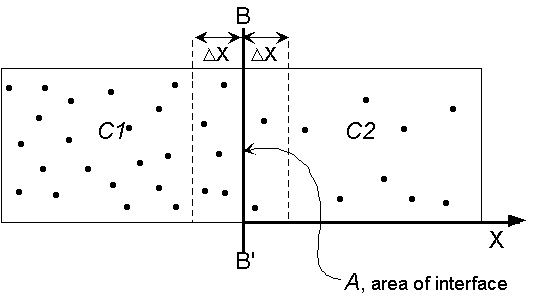
Within each time step, any particle
within a distance X of the interface B-B'
has a 50% probability of crossing over that interface. The number of particles
with the potential to cross B-B' from left to right (positive mass
flux) is (C1XA), where A is the area of interface B-B'. On average half of these take a positive step
and cross the interface in time t, such that the flux left to right is (0.5 C1x A). Similarly, the number
of particles crossing right to left in t (negative mass flux)
will be (0.5 C2X A). The resulting
mass flux, qX,,
is
(1)
.
If C(X) is continuous, then C2 
C1 + x 
C/x, and (1) becomes
(2)
.
X2/t is the coefficient of
diffusion, or diffusivity, and it units are [length2
time-1]. The diffusivity of a chemical molecule in
a given fluid depends on the ease with which the molecule can move, specifically,
how far, X, the molecule can move in a given time interval. The ease of molecular motion, and thus the
diffusivity of a particular chemical, will depend on the molecule size and
polarity, the type of fluid and the temperature.
Equation (2) is a mathematical expression of Fick's Law. Fick's Law states that the flux of solute mass crossing a unit area,
A, per unit time, t, in a given direction, e.g. X, is proportional to the gradient of concentration in that direction,
C/X, and is counter-gradient, i.e. the net flux is down-gradient. Because the flux in any direction is proportional only to the concentration
gradient in that direction, Fick's Law can be directly extended to three-dimensions.
(3) 
.
Note that for molecular diffusion, considered here, the coefficient for diffusion is isotropic, i.e. the same in all directions.
Diffusion from a point source
Consider a cloud of N particles (and total mass M)
released at X = 0 and t = 0.
Under the action of molecular diffusion, the cloud will slowly spread.
We use the random walk model to predict the distribution of particle
(mass) concentration , C(X,t).
Note, that if we assume a unit mass per particle, we can conveniently
interchange N = M. For simplicity we again consider a one-dimensional
system, with the same rules of random motion described above, i.e. at each time step, t, each particle will move either +X or -X with equal probability. Over time each particle will move a
bit forward and a bit backward. The
probable location of an individual particle after many such steps can be predicted
with the Central Limit Theorem (see any basic statistics text). Specifically, in the limit of many steps, the
probability that a particle will be located between
mX and (m+1) X approaches a normal
distribution with zero mean and a standard deviation of:
(4)
,
where, as above,
(5)
.
The probability that a particle ends up between X and X+X is
(6)
.
Now consider the full cloud of N particles. At any time t, the number of particles between X and X+X is expected to be n(X,t)
= N p(X,t)X. Thus, the concentration,
C, at position X is C(X,t)
~ n(X,t)/(AX), where A is the
constant cross-section of the one-dimensional system. Exchanging M for N, the concentration distribution, C(X,t), is
(7) 
=[mass / length3]
As noted above, this distribution is the normal distribution
with zero mean and standard deviation, 
, which should be familiar to you from any basic statistics
course. Briefly, the distribution
forms a bell-curve, as shown below. At
any time, sixty-eight percent of the total mass (total number of particles)
falls within ± 
of the mean position (X
= 0). Ninety-five percent of the
mass falls within ± 2 of the mean position.
And, 99.7% falls within ± 3 of the mean position.
Based on these limits, it has become common to define the extent of
a concentration patch based on the contour that includes ninety-five percent
of the total mass, i.e. the contour at 2 from the center. With
this convention the length of a diffusing cloud, L, is often taken as L = 4.
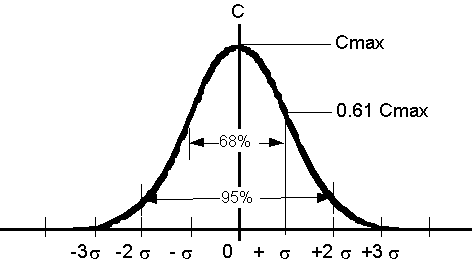
It is also useful to note that the concentration level at one standard deviation from the cloud center is 61% of the maximum concentration, i.e. C (X =
) = 0.61 Cmax,
where Cmax is
the concentration at the center of the cloud. This value provides a useful way to rapidly define the standard
deviation of a particle (species) cloud.
Example
of Random Walk Process:
This animation shows the motion of 500 particles in a one-dimensional
random walk with step size X = 1 in time t = 1. At t = 0
the particles are located at X = 0.
This random walk animation mimics the effect of Fickian Diffusion. As you watch the animation, consider the following.
Graph of Absolute Particle Location (lower left window).
This graph shows the number of particles located at each position of the X-axis. The number of particles per location is analogous to a concentration.
1) Over time how does the peak particle number, N, (concentration, C) change under the influence of random particle motion (diffusion)?
2) Over time how does the gradient in particle number (concentration), i.e. dN/dX (dC/dX) change under the influence of random particle motion (diffusion)?
3) What is the sign of the particle number (concentration) gradient (dN/dX) for X > 0? Consider the animation of individual particle motion (uppermost window). For X > 0, is the net particle flux positive (to the right) or negative (to the left)? Is the direction of flux up-gradient of down-gradient? Is the relationship between the direction of flux and the concentration gradient consistent with Fick's Law (equation 3)?
4)
Estimate the diffusion coefficient, D, using equation
(4) above, and the values of given in the upper
left corner of this graph. Note that
you can pause the animation. How does
the realized value of D compare with the theoretical value given in
equation (5). Note that no specific
units are given here, such that D will simply have unit L2T-1,
where L is an arbitrary length unit and T is the arbitrary time
unit.
Graph of Particle
Location in Terms of .
This graph plots the distribution of particle location with
the position normalized by the standard deviation, . The solid curve
is the Gaussian distribution.
5) Note that at early time (first few time steps) the real distribution of particles does not approximate a Gaussian distribution very well. This is because the Gaussian distribution is only valid after a sufficient number of steps (Central Limit Theorem). Use the animation to estimate how many steps are required for the distribution to consistently fit the Gaussian distribution.
Conclusion - Key Aspects of Diffusion
(7) Diffusion is the net flux due to random motion.
(8) Diffusive flux is proportional but opposite in sign to the gradient of concentration.
(9) Diffusion acts to dilute concentration and reduce gradients of concentration.