Convergence  Bisection Methods:  Bisection Methods:

The Error Criterion

Instead of the criterion |f(x)|< epsilon used above, we can implement criteria which are insensitive to the value of the function. One such criterion is obtained by requiring that |x₁-x₂|< delta. This is an absolute tolerance criterion. There are instances when this is not a good criterion to use. For example: suppose x₁ = 1.0000 and x₂ = 1.0001; then |x₁ - x₂| = 1.0E-4. Now, say the same equation was rescaled so that x₁ = 1.0000E+10 and x₂ = 1.0001E+10; then |x₁ - x₂| = 1.0E+6, a number much larger than the previous estimate before rescaling. This is not a desirable property for an error criterion. Hence in order to make the criterion independent of the absolute magnitude of x, we use a relative tolerance criterion, given by

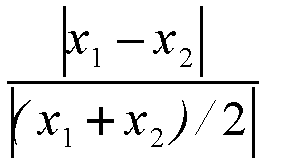(1)

 

Note that for both the intervals [1.0000,1.0001] and [1.0000E+10,1.0001E+10], we get a relative tolerance of 1.0E-4 .
 

1998-10-01