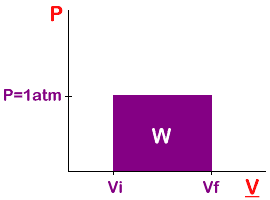
Work is the area in the rectangle.
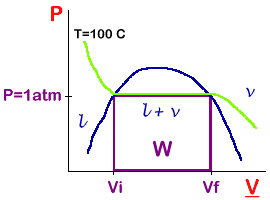
The l-v boundary and an isotherm at 100° is shown here.
One kilogram of liquid water at 100°C is vaporized to steam at 100°C in a piston. (Equilibrium can be assumed). What procedure is needed to determine how much heat would be required and how much work is done in this process? If Q does not equal W, what accounts for the difference?
Use the differential:
dW = PdV
The differential is based on the extensive (total) volume, not the intensive (per mole) volume.
| P-V Diagrams | |
|---|---|
|
|
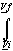 PdV
PdVSolve:
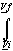 dV
dVLook up the volumes in a steam table
Since the volume of the liquid is negligible compared to the volume of the gas, we can ignore the initial volume of the liquid. That is, Vf >> Vi.
If we didn't ignore Vi:
Alternative method
Why does this diverge from our earlier answer?
We assumed that the vapor is an ideal gas. This turns out to be a poor assumption for water because water has strong hydrogen bonding not present in the ideal gas law assumptions.