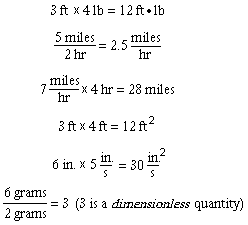
| Go To: | Section 2.1 | Units and Dimensions |
| Section 2.2 | Conversion of Units | |
| Table 2.3-1 | SI and CGS Units | |
| Section 2.3 | System of Units |
A measured or counted quantity has a numerical value (2.47) and a unit (whatever there are 2.47 of). It is useful in most engineering calculations -- and essential in many -- to write both the value and the unit of each quantity appearing in an equation:
2 feet, 1/3 second, 4.29 miles, 6 tomatoes, ...
A dimension is a property that can be measured, such as length, time, mass, or temperature, or calculated by multiplying or dividing other dimensions, such as length/time (velocity), length3 (volume), or mass/length3 (density). Measurable units (as opposed to countable units) are specific values of dimensions that have been defined by convention, custom, or law, such as grams for mass, seconds for time, centimeters or feet for length, and so on.
Units can be treated like algebraic variables when quantities are added, subtracted, multiplied, or divided. The numerical values of two quantities may be added or subtracted only if the units are the same:
3 ft - 1 ft = 2 ft (3x - x = 2x)
but
On the other hand, numerical values and their corresponding units may always be combined by multiplication or division:
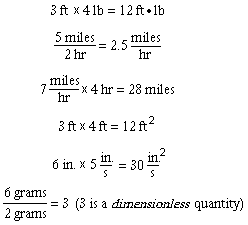
A measured quantity can be expressed in terms of any units having the appropriate dimension. A particular velocity, for instance, may be expressed in ft/sec, miles/hr, cm/year or any other ratio of a length unit to a time unit. The numerical value of the velocity naturally depends on the unit chosen.
The equivalence between two expressions of a given quantity may be defined in terms of a ratio:
Ratios of the form of Equations 2.2-1. 2. and 3 are known as conversion factors.
To convert a quantity expressed in terms of one unit to its equivalent in terms of another unit, multiply the given quantity by the conversion factor (new unit/old unit). For example, to convert 36 inches to its equivalent in feet, write
![]()
(Note how the old units cancel, leaving the desired unit.) An alternative away to write this equation is to use a vertical line instead of the multiplication symbol
![]()
Carrying along units in calculations of this type is the best way of avoiding the common mistake of multiplying when you mean to divide and vice versa. In the given example, the result is known to be correct because inches cancel out leaving only feet on the left-hand side, whereas
![]()
is clearly wrong. (More precisely, it is not what you intended to calculate.)
If you are given a quantity having a compound unit (e.g., miles/hr, calories/gram°C), and you wish to convert it to its equivalent in terms of another set of units, set up a dimensional equation: write the quantity and its units on the left, write the units of conversion factors that cancel the old units and replace them with the desired ones, then fill in the values of the conversion factors, and carry out the indicated arithmetic operations to find the desired value. (See Example 2.2-1.)
TEST YOURSELF
1. What is a conversion factor?
2. What is the conversion factor for s/min
(s = second)?
3. What is the conversion factor for min2/s2?
(See Equation 2.2-3.)
4. What is the conversion factor for ft3/in.3?
| Quantity |
|
|
| Length | Meter (SI) |
|
| Centimeter (CGS) |
|
|
| Mass | Kilogram (SI) |
|
| Gram (CGS) |
|
|
| Moles | Gram-mole |
|
| Time | Second |
|
| Temperature | Kelvin |
|
| Electric Current | Ampere |
|
| Light Intensity | Candela |
|
| Quantity | Unit |
|
Equivalent in Terms of Base Units |
| Volume | Liter |
|
0.001 m3 |
| 1000 cm3 | |||
| Force | Newton (SI) |
|
1 kg · m/s2 |
| Dyne (CGS) | 1 g · cm/s2 | ||
| Pressure | Pascal (SI) |
|
1 N/m2 |
| Energy, work | Joule (SI) |
|
1 N · m = 1 kg · m2/s2 |
| Erg (CGS) | 1 dyne · cm = 1 g · cm2/s2 | ||
| Gram-calorie |
|
4.184 J = 4.184 kg · m2/s2 | |
| Power | Watt |
|
1 J/s = 1 kg · m2/s2 |
2.3 SYSTEM OF UNITS
A system of units has the following components:
1. Base units, or units for the dimensions of mass, length, time,
temperature,
electrical current, and light intensity.
2. Multiple units, which are defined as multiples or fractions
of base units such as
minutes, hours, and milliseconds, all of which are
defined in terms of the base
unit of a second. Multiple units are defined for
convenience rather than
necessity: it is simply more convenient to refer
to 3 years than to 94 608 000
seconds.
3. Derived units, obtained in one of two ways:
(a) By multiplying and dividing
base or multiple units (cm2, ft/min,
kg
· m/s2,
etc.). Derived units of this type ar referred to as compound units.
(b) As defined equivalents of
compound units (e.g., 1 erg = 1 g
· cm/s2, 1 lbf
=
32.174 lbm · ft/s2).
In 1960 an international conference formulated a system of metric units that is rapidly gaining acceptance in the scientific and engineering community. It is known as the "Systeme Internationale d'Unites," or the SI system for short. Two of the base units of the SI system -- the ampere for electrical current and the candela for luminous intensity -- will not concern us in this book. A third, the degree Kelvin for temperature, will be discussed later. The others are the meter (m) for length, the kilogram (kg) for mass, and the second (s) for time.
Unit prefixes are used in the SI system to indicate powers of ten. the most common of these prefixes and their abbreviations are mega (M) for 106 (1 megawatt = 1 MW = 106 watts), kilo (k) for 103, centi (c) for 10-2, milli (m) for 10-3, micro (µ) for 10-4, and nano (n) for 10-9. The conversion factors between, say, centimeters and meters are therefore 10-2m/cm and 102cm/m. The principal SI units and prefixes are summarized in Table 2.3-1.
An SI convention is to use blanks rather than commas when writing large numbers: for example, 34 607 for 34,607. We will use this notation throughout the text.
The CGS system is almost identical to the SI system, the principal difference being that grams (g) and centimeters (cm) are used instead of kilograms and meters as the base units of mass and length. The principal units of the CGS system are shown in Table 2.3-1.
The base units of the American engineering system are the foot (ft) for length, the pound-mass (lbm) for mass, and the second (s) for time. This system has two principal difficulties associated with it. The first is the occurrence of conversion factors (such as 1 ft/12 in.) which, unlike those in metric systems, are not multiples of ten; the second, which has to do with the unit of force, is discussed in the next section.
Factors for converting from one system of units to another may be obtained by taking ratios of quantities listed in the table on the inside front cover of this book. A larger table of conversion factors is given on the inside back cover of the Chemical Engineers' Handbook1, and still another table is given on pp 1-24 through 1-27 of the Handbook.
TEST YOURSELF
1. What are the factors (numerical values and units) needed to
convert
(a) meters to millimeters?
(b) nanoseconds to seconds?
(c) square centimeters to square
meters?
(d) cubic feet to cubic meters?
(e) horsepower to British Thermal
Units per second?
2. What is the derived unit for velocity in the SI system? The
CGS system? The American engineering system?

_____________________
1 R.H.
Perry and C. H. Chilton, Eds., Chemical Engineers' Handbook, 5th
Ed., McGraw-Hill, New York (1973).