April 19, 2000

Problem:

Design biodegradable polymer drug release systems for the cases of (a) essentially constant drug release rate, and (b) increasing drug release rate. For each case describe the properties of the materials used and the shape of the system chosen. Maximum credit is given for the simplest solution.

Solution:

Of the design types covered in lecture (reservoirs, matrices, pendant chains, swelling control, and osmosis control) the simplest to construct using biodegradable polymers is a matrix. The basic design principles, advantages, and disadvantages were shown on pp. 15-16 in the “Advances in Controlled Release Technology” handout.

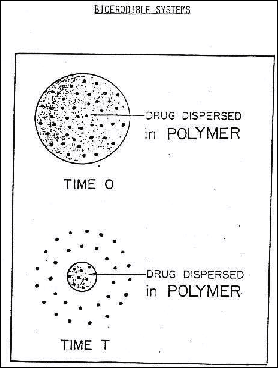
From the handout, for both design cases the properties of the biodegradable polymer should be:

- erosion only at the surface (as in the “soap bar” model described in class)

- non-toxic byproducts of degradation

- rate of diffusion of drug through polymer very small relative to rate of degradation of the polymer, so that an even distribution of drug in the matrix can be maintained

Also from the handout, the rate of drug release will be directly proportional to the exposed surface area of the biodegradable polymer.

a) Essentially constant drug release rate

Because of the proportionality mentioned above, for this case we want to use a system that will have an eroding surface with a total area that remains essentially constant over time. There are at least two simple designs capable of achieving this. The first is a very flat disk or slab.

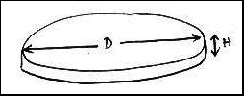
The surface area here is given by

If we assume that erosion occurs at the same rate at all faces, then the drug release rates over time for cases of different D:H ratios is shown below.

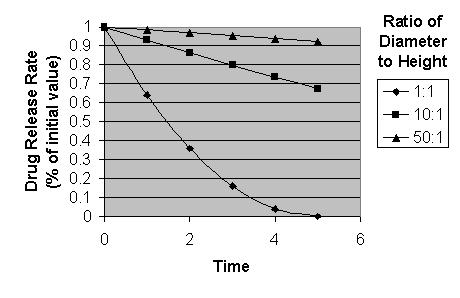
As the device becomes thinner, the surface area, and resulting drug release rate, becomes more constant over time.

A second simple design involves a hollow cylinder.

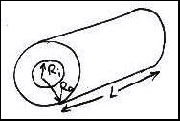
The surface area here is given by

As with the thin disk described above, we can assume that erosion occurs at the same rate at all faces, and we can design the device such that the ratio of L:R is very large. Then the sum of the two radii will remain constant because R_i will be increasing at the same rate as R_o will be decreasing. Also, the percent change in the length will be small relative to the percent change in each of the radii. The net result will again be a surface area that does not change significantly over time.

b) Increasing drug release rate

For this case we want to use a system that will have an eroding surface with a total area that increases over time. To do this, the design must incorporate surfaces that are coated with a polymer that is significantly less biodegradable than that of the polymer used to form a matrix with the dispersed drug. One example of such a design is a cone- or pyramid-like shape in which the base and sides are prevented from eroding by this coating, and the “point” end is allowed to erode and grow larger over time.

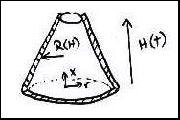
The surface area here is given by

Over time, the top surface will erode and H will decrease. This will cause an increase in R, which will expose a larger surface area of polymer/drug matrix, which will increase the rate of drug release.

Grading:

Design for case (a) – 4 pt

Design for case (b) – 4 pt

Polymer choice:

surface erosion only – 1 pt

insignificant drug/polymer diffusion – 0.5 pt

non-toxic polymer degradation byproducts – 0.5 pt