10.491: Integrated Chemical Engineering

Prof. Robert Langer

Problem Set 2

May 1, 2000

Problem:

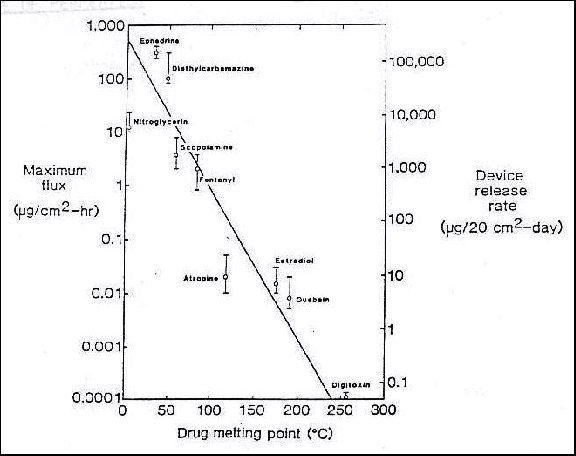
Data has shown that the flux of drug from a transdermal delivery system decreases logarithmically as the melting temperature of the enclosed drug increases. Is there an explanation for this, and if so, what is it? Hint: Consider the thermodynamics of the system.

Solution:

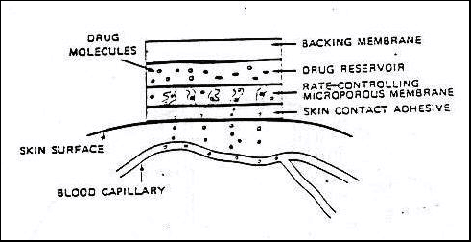
A schematic of a typical transdermal drug delivery system is shown in the figure below. The drug is loaded into a reservoir, most often in a supersaturated solution to maintain a constant dissolved drug concentration, from which it diffuses through a polymeric membrane and the patient’s skin. To decrease the influence of patient-to-patient variability, the device is designed such that the diffusion through the polymer is the rate-limiting step. Because the drug is assumed to nearly instantly disperse upon penetration into the blood stream, the internal concentration of drug is considered to be negligible and the body is treated as an “infinite sink.”

The general form of the equation describing flux in the a system with supersaturated drug and an infinite sink is

where F is flux, D is the diffusivity constant, K is the partition coefficient, C_S is the drug solubility, A is the surface area, and L is the length through which the drug must diffuse. Of these parameters, D, K, and C_S will be affected by the properties of the drug, and C_S will be influenced the most strongly by the drug's melting temperature. The ideal law of solubility gives the relationship between solubility and melting temperature. What follows is a description of the derivation of this relationship.

If we assume that the drug is present in a supersaturated dispersion in the device, then the solid and liquid drug must be in chemical equilibrium with one another with

This assumes that the solid is pure drug and the liquid has a mole fraction x_D of drug. If we also assume that the liquid solution behaves ideally, then from the definition of an ideal solution we have

with μ_L^o signifying the chemical potential of the pure liquid drug. Combining (2) and (3) gives

From the definition of the Gibbs energy of fusion of a pure liquid at temperature T and pressure P,

(5)

Combining (4) and (5) gives

Differentiating by x_D at constant P gives

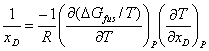(6)

From the definition of Gibbs free energy,

(7)

Differentiating by T at constant P gives

(8)

From the definition of enthalpy,

(9)

From the first law of thermodynamics for closed, reversible systems,

(10)

From the definition of reversible mechanical work,

(11)

From the definition of entropy,

(12)

Combining (10)-(12) gives

(13)

Combining (9) and (13) gives

Taking the partial derivative with respect to T at constant P gives

(14)

Combining (8) and (14) gives

(15)

Also, differentiating G/T by T at constant P gives

(16)

Combining (15) and (16) gives

(17)

Combining (7) and (17) gives

(18)

This is the Gibbs-Helmholtz equation. Combining (6) and (18) gives

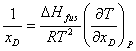
Integrating from the case of pure drug with the freezing/melting point T_m to drug in solution with freezing/melting point T, assuming ΔH_fus is constant from T_m to T, gives

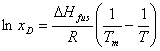
This is the ideal law of solubility. From the equation it can be seen that as T_m increases, the mole fraction of drug in solution, x_D, decreases logarithmically. Because the concentration of drug in solution in the device drug reservoir is proportional to x_D, C_S will also decrease with increasing T_m. From equation (1), then, this will result in the logarithmically decreasing trend seen in the graph of the problem statement.