10.491:
Integrated Chemical Engineering
Prof. Noah
Lotan
Problem Set 3
May 8, 2000
Solution:
Problem 1
From lecture, for the case
in which
-
the
body is modeled as a true CSTR
-
the
total concentration of the feed stream is always constant
-
the
feed stream is 100% B at t<0
-
the
feed stream is 100% D at t≥0
we have
![]() (1)
(1)
![]()
![]() (2)
(2)
Plotting equations (1) and (2) for the three pairs of F and V given in the problem statement gives
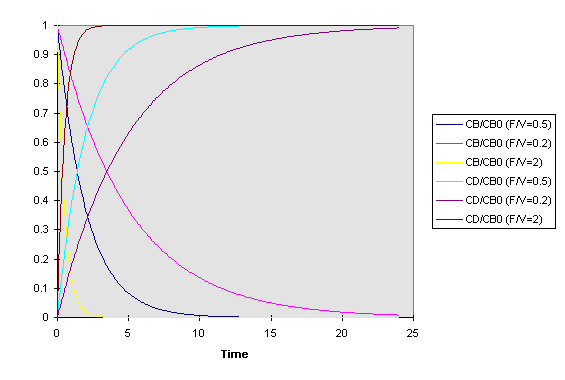
From
the figure it can be seen that as the value of F/V increases, the
replacement of B in the body by D occurs at a faster rate. This is because in
these cases the residence time of the tank is reduced, with B and D requiring
less time to pass through the body.
Problem
2
Solving
equation (2) for t gives
![]() (3)
(3)
Using data set 1, with V=4 l, F=2 l/h, and CD/CB,0=CD,tox/CB,0=0.7/1=0.7, in equation
(3) gives t=2.41 h. This will be the
time required for the concentration of D to initially reach a toxic
concentration in the body.
In the next step of the process, because D is being
flushed from the system, it will show a profile exactly like that of B in
Problem 1. We can then solve equation (1) for t and replace the concentration terms with those representing D,
giving
![]() (4)
(4)
Solving equation (4) with the values V=4 l, F=2 l/h, and CD/CD,0=CD,eff/CD,tox=0.2/0.7=
0.29, gives t=2.48 h. This will be
the time required for the concentration of D to drop from the minimum toxic
concentration to the minimum effective concentration.
The final calculation again involves an increasing
trend in D, so equation (3) will be used. Solving equation (3) with V=4 l, F=2 l/h, and CD/CD,0=(CD,tox-CD,eff)/(CD,in-CD,eff)= 0.5/0.8=0.625, gives t=1.96 h. This will be the time required for the concentration of D
to increase from the minimum effective concentration back up to the minimum
toxic concentration.
All other sections of the treatment protocol will
simply involve repeating the second and third steps described above. From the
calculated times, and those calculated using the values of data set 2, we can
then fully describe the process.
|
|
Data Set 1 |
Data Set 2 |
|
t1 |
2.41 h |
1.20 h |
|
t2 |
4.89 h |
1.44 h |
|
t3 |
6.85 h |
1.61 h |
|
t4 |
9.33 h |
1.85 h |
|
t5 |
11.29 h |
2.02 h |
From the table it can be seen that as the
therapeutic range of the drug narrows,
the administration schedule requires more frequent changes from feeds of 100% B
to those of 100% D and back again.
Problem 3
From lecture, for the case
in which
-
the
body is modeled as two true CSTRs in series
-
the
total concentration of the feed stream is always constant
-
the
feed stream is 100% B at t<0
-
the
feed stream is 100% D at t≥0
we have
![]() (5)
(5)
![]()
![]() (6)
(6)
Plotting equations (5) and (6) for the two-CSTR case of F=2 l/h and V=2 l, and the one-CSTR case of F=2 l/h and V=4 l, gives
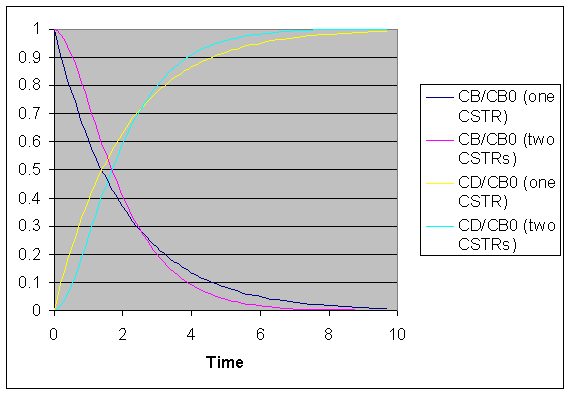
From the figure it can be seen that for the case of
a two-CSTR model, a longer period of time than in the case of the one-CSTR
model is required for the replacement of B in the body by D. At later times,
however, this replacement occurs at a faster rate with the two-CSTR model than
with the one-CSTR model. The initial lag is caused by the extra time needed for
changes in the concentrations of the first of the two CSTRs to affect the
concentrations of the second tank. The later higher rate is caused by the
smaller residence time of the second tank compared to that of the single tank
of the one-CSTR model.