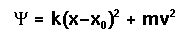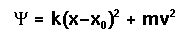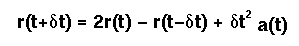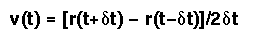A Simple Harmonic Oscillator
The harmonic oscillator example can be used to see how molecular dynamics works in a simple case. The equation of motion describing the dynamic behavior in this case is:
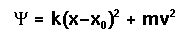where 0.5k(x-x0)^2 is the potential energy contribution and 0.5mv^2 is the kinetic energy contribution. x is the displacement of the oscillator from equilibrium, x0, v is the velocity of the oscillator, and m is its mass. k is the spring constant. The force (f) acting on the mass at any time is k*(x-x0), so the acceleration (a) may be computed using the relation: f = m*a = k*(x-x0).
There are numerous ways to step through the trajectory of motion of the oscillating mass. All make use of Finite Difference methods to update the position, velocity and acceleration of the oscillator at some future time t+dt, based on current information about the position, velocity and acceleration at the current time t and earlier times.
- The Verlet Algorithm is probably the most commonly used one. It actually makes use of the position at time t, the acceleration at time t, and the position at time t-dt, to estimate the position at time t+dt.
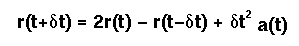
Velocity information is not used directly, but may readily be estimated:
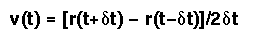
There are several variants of the basic Verlet Algorithm (see pg 287 of Rowley, Statistical Mechanics for Thermophysical Property Calculations, Prentice Hall: Englewood Cliffs, 1994).
- Predictor Corrector methods are usually more accurate. The most common is the Gear Predictor-Corrector. This is a two-step method that first makes an estimate of the changes at time t+dt, and then uses these estimates to improve the accuracy of the step.
A C programwhich implements the Verlet Algorithm to step through the dynamics of a harmonic oscillator is available for browsing. To see the program in action, click here The results are displayed graphically using the relative displacement of the oscillator from equilibrium as the ordinate, and the fraction of the total energy of the oscillator which is stored as potential energy (or any one of four other options) as the abscissa. (This display is generated using SGI's GL graphics library and may not be compatible with all computer systems.)
In the chemical world, the vibrational motion of covalent bonds are often approximately harmonic. For example, a simple diatomic molecule has exactly one bond, whose length is the distance between two atoms which are moving with kinetic energy but are drawn to each other by covalent bonding forces. (At very short distances, this attraction becomes a repulsion as the nonbonding orbitals of each atom begin to overlap.) The distance between atoms describes a harmonic oscillation at finite temperatures.
UP one level