Up to now - Vector Data Models (model boundaries of spatial features)
- Vector Feature Types:
- Points
- The fundamental building block
- Lines
- Built from at least two points at the ends of the line: the nodes
- Extra points between the nodes--vertices--may add shape to the line
- Polygons
- A closed object with an interior and exterior
- Built from one or more lines
- May have islands
- Vector Data File Formats:
- ArcGIS Shapefiles
- .shp, .shx, .dbf files (and possibly others)
- Topological relationships are not stored in the layer, but computed on the fly when needed
- Shapefiles are easily moved or copied within the OS; just copy or move layer.*
- Other vector-based data models
- ArcInfo coverages
- stores topological relationships
- shared points and lines
- Standards: Open Geospatial Consortium protocols for web services and Application Programming Interface(Web Mapping Service and Web Feature Service); Geographic Markup Language (GML) for xml-based data interchange (and the KML subset used by Google); etc.
- very prolific (1700 projects over career) and influential
- helped create U.S. National Park System
- wrote first "National Plan" advocating conservation areas as
well as development
- resource-based planning (natural characteristics should influence city form) "multiple neighborhood-based centers determined by available resources"
- importance of parks: "the cities that are best designed have about one-eigth of their area in parks and about one acre to 75 people." (Manning 1919)
- Differed from "City Beautiful movement" which emphasized monumental civic centers and public buildings
- mapped natural resources by survey (no airphotos!)
- used light tables and hand tracing for spatial analysis
- characteristics might be "good" in which case overlap areas are "suitable"
- characteristics might be "bad" in which case overlap areas are "unsuitable"
- characteristics might be "medium good" or "pretty bad" for
intermediate cases
-
Why not do overlays with Vector Model?
- "Sliver problem" doesn't scale well
- In an analysis with dozens of layers, can spend as much time on cleanup as analysis
- Speed / Efficiency
- Vector data model, particularly with polygons, is complex ("simple" overlay requires many computations)
- Raster data model is a very efficient representation inside digital computers
- Discrete objects / legal boundaries versus Natural gradients
- Many natural features are very hard logically to delineate
(because consequence of continuous processes)

- Many natural features are very hard logically to delineate
(because consequence of continuous processes)
- "Sliver problem" doesn't scale well
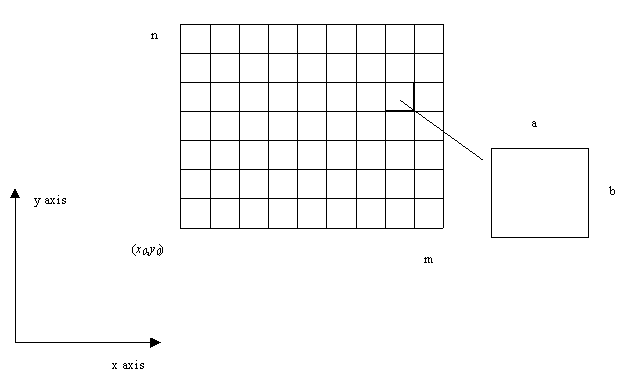
- Typically represented as a two-dimensional X-Y array
- Useful notes on raster models: see online 'Core Curriculum in
Geographic Information Science':
- http://escholarship.org/uc/item/3g1217wg?query=ncgia%20giscience
- Download PDF and see "Representing Fields" in Chapter 2, Section 2.4
- More dimensions (Z for height, T for time) also possible, but harder to visualize
- Most rasters assign a single scalar value to each grid cell
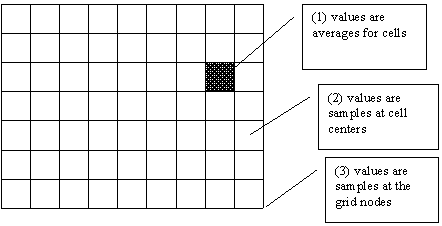
- Value of the cell may represent (Goodchild's Illustration):
- an average value over the entire cell area
- the value at the center of the cell (ArcGIS does it this way)
- the value at a grid corner
- Possible to have multiple values--a vector of values--assigned to each cell
- Georeferenced images (e.g., orthophotos) are another type of raster data
- Orthophotos (2m x 2m; 0.5m x 0.5m)
- Cell value is pixel brightness in orthophoto
- Scanned maps - e.g., ESRI street maps and orthophoto web services that we used in labs
- ArcGIS (and earlier ArcView) use a common raster data format
called a grid
- This is the default representation
- Has odd naming restrictions (based on Fortran): 13 characters + underscore
- Can also use "geoTIFF" simply by specifying extension (output: this_is_my_long_descriptive_filename.tif)
- ArcGIS's toolkit for raster analysis is the optional (and
expensive) Spatial Analyst extension
- Can view rasters in base version, but not manipulate
Raster Data Models (model properties of uniformly spaced grid cells)
Historical Motivation
General Concept of Site Suitability Analysis (i.e., appropriate land use based on characteristics of land)
Warren Manning, student of Frederick Law Olmstead, active early 20th century
Key intellectual ideas:
How to implement these ideas in a predigital world? (not easy!)
Use overlays of maps to determine areas where characteristics overlap
Manning's Ideas & Methods Revisted and Popularized in 1960s by Ian McHarg (Penn) and Carl Steinitz (Harvard)
Raster Data Model
Illustrating basic raster operations in ArcGIS - brief demo...
- Feature-to-raster tool (in ArcToolbox) to convert Cambridge block
group polygons into a raster layer
- 100 meter grid cells
- use median housing value for value in each raster grid cell
- IDW interpolation tool (in ArcToolbox) to Interpolate prices in
sales89 to get a housing value 'surface'
- Inverse-distance-weighted average of 12 closest sales
- Attending to the particulars
- getting the grid in the right place (extents...)
- getting the cell size right (coordinates and dimensions...)
- masking off the parts not in Cambridge
Comparing Field and Object Models
- Each feature is a discrete object with vectors representing object boundaries
- "treats the information space as populated by discrete, identifiable entities, each with a georeference" (Worboys, p. 149)
- Labels discrete chunks of space and records the properties of each chunk
- Good where values vary continuously over space; the raster approximates these variations with discrete "samples"
- "[geographic] information as collections of spatial distributions" (Worboys, p. 149)
- Examples:
- Temperature
- Rainfall
- Elevation
- Depth
- Concentration of a chemical in the air, water, or soil
- Fields are actually functions that map spatial locations to values
- Representing continuously varying 'fields'
- Representing fields (Goodchild's discussion)
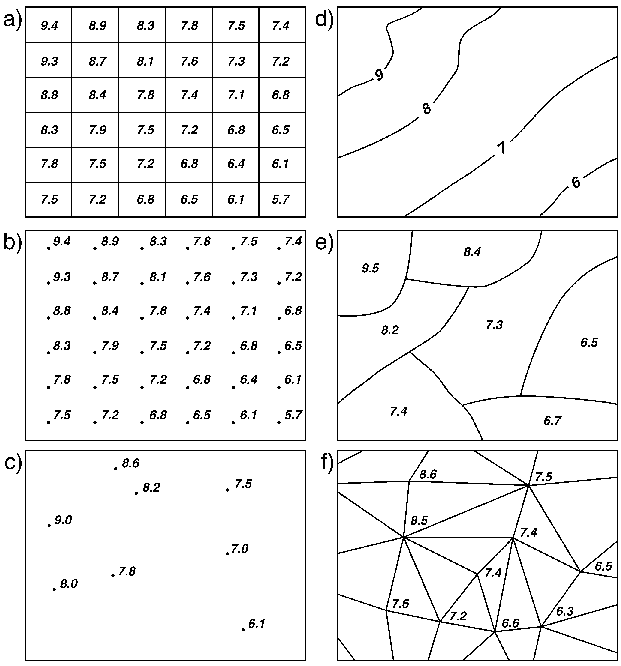
- Different field representations (Goodchild's illustration):
- Weather modeling example at the National Center for Atmospheric
Research (NCAR):
MM5 (mesoscale model, fifth-generation)
Object (Vector) Model
Field (Raster) Model
a) rectangular cells d) digitized contours b) rectangular grid of points e) polygons c) irregularly spaced points f) triangulated irregular network (TINs)
Types of Rasters
Technical Formats
Integer
Commonly "8 bit" meaning up to 255 discrete types can be stored
Sometimes 16 bit, so many more discrete values can be stored (~65,000)
Floating Point
Similarly, can be either "single precision" (float)
Double precision (double)
Logical Types
Discrete values of a continuous variable (inches of precipitation rounded to nearest inch)
Continuous representation of a continuous variable ( inches of precip as floating point, i.e. 2.534634)
Binary Maps Representing Presence/Absence (frequently coded as 1=present, "NoData" or 0 = absence)
Thematic classifications (numbers used arbitrary, meaning comes from key/value associations, i.e. 12 = residential)
Examples / Common Raster Data Uses
- A digital elevation model
- values denote elevation of each cell's center point (above mean sea level in meters)
- Source many you have seen already: USGS STRM global and national elevation data
11 12 13 14 2 2 4 16 1 1 2 12 12 11 12 13
Example of elevation rounded to nearest meter (continuous variable, discrete representation)
- Output from one band of a remote sensing satellite (or a panchromatic aerial photo)
- gives the level of radiation received by the satellite in that band, recorded as a number between 0 and 255 (8-bit)
14 10 11 74 12 12 77 92 12 78 90 91 70 90 94 90
Example of hypothetical remote sensing channel
"Features" are not discrete. Some categories of land use have same color/spectral characteristics (i.e. roads and roofs)
- A classified scene in which satellite output has been assigned to one of a number of classes denoting various land uses
- e.g. 1=urban, 2=cultivated land, 3=water.
- many image processing and pattern recognition algorithms are used to classify/categorize imagery
- field commonly known as "Remote Sensing" (start with multispectral image + sample areas of known type, endpoint is thematic map of land cover)
Start with image band above (and probably other bands representing other spectral ranges)
End up with discrete "land cover" classification
1 1 1 2 1 1 2 3 1 2 3 3 2 3 3 3
(for example 1=corn, 2=road, 3=forest)
- A representation of the presence of roads
- e.g. 1=road present, 0=no road
0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0
- A flood plain map
- value = 50 if greatest flood risk in cell is 1-in-50 year flood; 100 if 1-in-100 year flood; etc.
100 100 100 100 100 100 100 100 50 50 50 50 50 50 50 50
Creating Raster Maps
Two major methods:
Classifying raw imagery
Using Remote Sensing (beyond scope of this class, but important, powerful, semiautomated technique)
"By Hand" such as in Photoshop with Magic Wand Tool (not standard professional method, but gives a good understanding of issues)
Rasterizing Digitized Vector Features from CAD or GIS
Why?
Design with nature.
Do your unified analysis of natural features represented using raster with vector boundsExamples: which parcels have average slope > 15%
which census blocks are prone to flooding?Efficiency in large area studies
Example: Calculating stream buffers for every stream in Oregon
In vector Arc/Info, 2+ days of processing time
In raster grid, <1 minute for same stream network
Raster Analyses: Neighbors and 'Map Algebra'
- Edge-neighbors are four neighboring cells that share an edge with
the cell. ('rook' adjacency)
0 1 0 4 X 2 0 3 0
Which cells are "adjacent" to the road? using a "4-connected rule" ('queen' adjacency)
Adding diagonals yields eight-nearest neighbors (nine including original cell)1 2 3 4 X 5 6 7 8
Subtle but important: which cells are "adjacent" to the central cell? (decision rule not in normal parlance affects answer)
- Map Algebra (phrase coined by Dana Tomlin)
- Often useful to compute algebraic function of neighbors
- Smooth distributions (recompute cell value to be average of neighbors)
- Model water flow (accumulate water from neighbors that are higher up)
- Plume dispersion model
- Useful to construct new raster layer where each cell's value is an algebraic function of neighbors
- The regular structure of the grid cells can simplify spatial modeling and analysis
- Often useful to compute algebraic function of neighbors
Raster Difficulties
Edge Effects
- Some cells on the border that have only two or three edge-neighbors.
- Map algebra models will behave differently at a boundary where there are fewer neighbors - edge effects
- Common fixes for edge effects
- Run the model with an expanded coverage area for the raster, but then throw away the borders.
- Weight cells to compensate for missing neighbors (but difficult to determine the weight)
- Declare that a cell on the bottom border of the raster actually neighbors a cell on the top border.
When NOT to Use Raster Representations
- Rasters are less useful for representing networks where topology/connectivity is important and can't be captured at grid cell scale
- Example 1: modeling sewer lines as a raster layer
- code 1 in cells where a sewer is present, 0 elsewhere
- if two adjacent cells both have 1, that's no guarantee the sewers they contain are connected
- Example 2: Representing land ownership parcels as a raster layer
- by definition, the boundary between two survey points is a mathematically straight line
- the jagged appearance of a raster representation might be unacceptable or raster resolution required to represent might be impractical
- Rasters cell size is a direct indicator of level of geographic detail
- Sometimes a plus - better indication of relevant data resolution
- To double spatial resolution, there may be four times as many cells
Raster <-> Vector Conversions
- Possible, and supported by ArcGIS
- Not symetrical
- Vector to raster is easy, deterministic
- Raster to vector is harder - decisions needed, sometime scale-sensitive
General Strategy
- Try to keep original GIS data in native format
- Convert data as necessary for analyses, including vector to raster
- Convert data back to vector when useful (example: summarizing max slope per parcel)
Example: Manipulating terrain and land cover in Raster
- Elevation
- Reclass of absolute elevation into 5 categories
- Reclass of absolute elevation, pulling out "low elevation"
- Slope
- One step easy operation in GIS
- How does it work?
- Why is it important? (basic for building suitability constraint, important for erosion/hydrology)
- Aspect
- Also easy one-step operation in GIS
- Important for solar access studies, microclimate-based siting, vegetation prediction
Suggested Additional Readings on Raster Models
The NCGIA Core Curriculum in GIScience Unit TOC Section Unit Author Table of Contents (TOC) Representing Fields 2.4 054 Michael F.Goodchild Rasters 2.4.1 055 Michael F. Goodchild Representing Networks 2.6 064 F. Benjamin Zhan Worboys, Michael F. GIS: A Computing Perspective. London: Taylor & Francis, 1995.
Chapter 4: Models of Spatial InformationMore abstract, general, and mathematical than the NCGIA core curriculum notes(Minimal discussion of raster models in the Ormsby 'Getting to Know ArcGIS' book)
Created by Joseph Ferreira, Jr., 3 November 1999
Extensively rewritten for Fall 2000 by Thomas H. Grayson
Modified 2004-06 by Joseph Ferreira, Xiongjiu Liao, and Michael Flaxman
Last modified 13 March 2018 by Joseph Ferreira
Back to the 11.188 Home Page.
Back to the CRON Home Page.