lecture 24A

13.021 – Marine Hydrodynamics

Lecture 24A – Lifting Surfaces

Introduction

Lifting surfaces in marine hydrodynamics typically have many applications such as hydrofoils, keels, rudders, propeller blades and yacht sails. A lifting surface is a thin streamlined body that moves in a fluid at a small angle of attack with a resultant lift force normal to the direction of flow.

Consider the foil in figure 1in a uniform free stream. The straight line joining the center of curvature of the leading edge to the trailing edge is the chord. The camber line is midway between the upper surface and the lower surfaces. The distance between the chord and the mean camber line is the camber. The angle a between the free stream and the chord line is called the angle of attack.

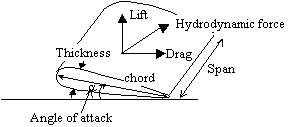
Figure 1 – Dimensions of foil

The hydrodynamic force that points in the direction of the free stream is defined as the drag force, while the component normal to the free stream in the upward direction is the lift force. The lift and drag forces vary with the angle of attack. These forces are expressed nondimensionally by defining the coefficients of lift and drag with respect to the planform area A.

Models of Reality

All bodies in real life are best modeled as 3D objects. Assume a smooth body of arbitrary shape is placed in a steady, irrotational flow field with zero viscosity. D’Alembert states that in 3D, there are no vector forces existing on the body; no lift and no drag. Solving Laplace’s equation in 3D and the boundary value problem (BVP) gives a unique solution where the circulation is zero.

However, the case of zero vector forces everywhere is a little boring and it is often difficult to solve 3D problems and 2D modeling is often more appropriate. Flows around a foil are usually treated as two-dimensional problems where it is assumed that the span is infinite. For steady flow of an unbounded fluid without vorticity over a 2D body, Laplace’s equation and the BVP do not have a unique solution because a circulation G can always be found as a solution. Then with a circulation G that will not violate Laplace’s equation and the BVP in a uniform flow, D’Alembert states that there is still zero horizontal force (zero drag) but G will produce lift.

Another way to understand that there is no drag force on the foil is to look at energy conservation in a potential flow. Recall that if drag existed on the foil, energy would be fed continuously into the fluid as the foil moved at a steady velocity and did work on the fluid against the drag force. But in the potential flow there is no viscosity and hence no way to dissipate the energy the foil would be adding to the fluid. Since we are assuming the problem is steady in a reference frame fixed with the foil, dE/dt = 0.

In other words, the energy E of the fluid is not changing with time. Therefore the foil cannot be continuously adding energy to the fluid, since there is no dissipation to balance the energy addition, and this in turn means that the foil is not working against any drag force.

For the case of a foil at an angle of attack a in an ideal irrotational flow, potential theory prescribes that the velocity of the sharp trailing edge is infinite since this is an external corner flow. Stagnation points exist at the leading edge and on the upper surface of the foil near the trailing edge.

Figure 2 – Ideal flow about a foil

Circulation

If the stagnation point on the body is specified, this will result in a fixed circulation G, which will specify the amount of lift produced. Similarly, if G is specified, this will fix the stagnation points and produce a specific lift force. The body is still in a steady, irrotational, inviscid flow; drag remains zero in either case.

Since lift is required, how can we specify the stagnation point at a fixed point on the body? The first step is to choose the ideal body configuration. For a body that is not foil-shaped, or streamlined, flow separation can occur from the surface of the body, reducing the circulation and associated lift. It was observed that a foil-shaped object helps guide the flow around the body so that it does not separate until it leaves the trailing edge.

Real fluid particles cannot move at infinity relative to each other due to viscous effects (particles exert shear forces on each other) and therefore the flow around the trailing edge will have a finite velocity. Since real flows tend to separate when rounding a corner, like the trailing edge of a foil, the ideal body shape is a foil positioned so that it causes the flow to leave the trailing edge at a finite velocity in a smooth tangential manner. This is known as the Kutta condition and is satisfied at small angles of attack.

From experiments, it was observed that at an angle of attack of 0 to 10 degrees, the flow detaches at roughly the trailing edge on the foil, resulting in a maximum lift range.

How much Lift?

So, how much lift will be generated using potential flow theory if the stagnation point is at the trailing edge of the foil? Now the 2D boundary value problem is specified as:

Perturbation potential:

Total Potential:

Governing Equation:

K.B.C. on the foil:

At infinity:

Kutta condition:

This BVP now has a unique solution and thus a unique lifting force for the given stagnation point at the trailing edge (T.E.).

From the solution of f of this BVP, we can then obtain the resulting G and associated lift force from the Kutta-Joukowsky theorem.

Kutta-Joukowsky theorem (2D):

A simple proof of the Kutta-Joukowsky theorem for a thin foil (thickness << chord) can be obtained as follows:

Let a be small enough so that every point on the foil surface is almost parallel to the direction of flow. The upward force per spanwise unit length on the element dx is

where and are the pressures on the lower and upper surfaces of the foil.

Bernoulli’s equation gives:

For a thin foil, the variations of the velocity from the free-stream velocity U will be small and we may approximate this by

Hence the total lift per unit span is:

The circulation physically around a contour and just outside the boundary layer may be approximated by

Thus by comparison, which gives the Kutta-Joukowsky theorem.

From the above demonstration, we see that for a lifting force to exist on a foil, the pressure on the upper surface of the foil must be diminished and the velocity increased relative to the pressure and the velocity on the lower surface of the foil, producing a net upward force. These pressure and velocity changes are a result of circulation.

REFERENCES

1- Fluid Mechanics with Engineering Applications - Daugherty

2- A first course in fluid dynamics - Patterson

3- Fluid Mechanics for Engineers - P.S. Bana 1969

4- Fluid Mechanics: A Laboratory Course - Plint/Boswirth

5- Marine Hydrodynamics, J. N. Newman

7- Physical Fluid Dynamics, D. J. Tritton