Theory of Flight

Flight is a phenomenon that has long been a part of the natural world. Birds fly not only by flapping their wings, but by gliding with their wings outstretched for long distances. Smoke, which is composed of tiny particles, can rise thousands of feet into the air. Both these types of flight are possible because of the principles of physical science. Likewise, man-made aircraft rely on these principles to overcome the force of gravity and achieve flight.

Lighter-than-air craft, such as the hot air balloon, work on a buoyancy principle. They float on air much like rafts float on water. The density of a raft is less than that of water, so it floats. Although the density of water is constant, the density of air decreases with altitude. The density of hot air inside a balloon is less than that of the air at sea level, so the balloon rises. It will continue to rise until the air outside of the balloon is of the same density as the air inside. Smoke particles rise on a plume of hot air being generated by a fire. When the air cools, the particles fall back to Earth.

Heavier-than-air flight is made possible by a careful balance of four physical forces: lift, drag, weight, and thrust. For flight, an aircraft's lift must balance its weight, and its thrust must exceed its drag. A plane uses its wings for lift and its engines for thrust. Drag is reduced by a plane's smooth shape and its weight is controlled by the materials it is constructed of.


Lift

In order for an aircraft to rise into the air, a force must be created that equals or exceeds the force of gravity. This force is called lift. In heavier-than-air craft, lift is created by the flow of air over an airfoil. The shape of an airfoil causes air to flow faster on top than on bottom. The fast flowing air decreases the surrounding air pressure. Because the air pressure is greater below the airfoil than above, a resulting lift force is created. To further understand how an airfoil creates lift, it is necessary to use two important equations of physical science.

The pressure variations of flowing air is best represented by Bernoulli's equation. It was derived by Daniel Bernoulli, a Swiss mathematician, to explain the variation in pressure exerted by flowing streams of water. The Bernoulli equation is written as:

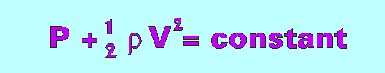
where:	 P = pressure (force exerted divided by area exerted on)
	 rho = density of the fluid
	 V = velocity of the moving object or fluid

To understand the Bernoulli equation, one must first understand another important principle of physical science, the continuity equation. It simply states that in any given flow, the density (rho) times the cross-sectional area (A) of the flow, times the velocity (V) is constant. The continuity equation is written as:

where:	P = pressure
	V = velocity
	A = cross sectional area of flow

Using the Bernoulli equation and the continuity equation, it can be shown how air flowing over an airfoil creates lift. Imagine air flowing over a stationary airfoil, such as an aircraft wing. Far ahead of the airfoil, the air travels at a uniform velocity. To flow past the airfoil, however, it must "split" in two, part of the flow traveling on top and part traveling on the bottom.

The shape of a typical airfoil is asymmetrical - its surface area is greater on the top than on the bottom. As the air flows over the airfoil, it is displaced more by the top surface than the bottom. According to the continuity law, this displacement, or loss of flow area, must lead to an increase in velocity. Consider an airfoil in a pipe with flowing water. Water will flow faster in a narrow section of the pipe. The large area of the top surface of the airfoil narrows the pipe more than the bottom surface does. Thus, water will flow faster on top than on bottom. The flow velocity is increased some by the bottom airfoil surface, but considerably less than the flow on top.

The Bernoulli equation states that an increase in velocity leads to an decrease in pressure. Thus the higher the velocity of the flow, the lower the pressure. Air flowing over an airfoil will decrease in pressure. The pressure loss over the top surface is greater than that of the bottom surface. The result is a net pressure force in the upward (positive) direction. This pressure force is lift.

There is no predetermined shape for a wing airfoil, it is designed based on the function of the aircraft it will be used for. To aid the design process, engineers use the lift coefficient to measure the amount of lift obtained from a particular airfoil shape. Lift is proportional to dynamic pressure and wing area. The lift equation is written as:

where S is wing area and the quantity in parantheses is the dynamic pressure. In designing an aircraft wing, it is usually advantageous to get the lift coefficient as high as possible.

Drag

Every physical body that is propelled through the air will experience resistance to the air flow. This resistance is called drag. Drag is the result of a number of physical phenonmena. Pressure drag is that which you feel when running on a windy day. The pressure of the wind in front of you is greater than the pressure of the wake behind you. Skin friction, or viscous drag, is that which swimmers may experience. The flow of water along a swimmer's body creates a frictional force that slows the swimmer down. A rough surface will induce more frictional drag than a smooth surface. To reduce viscous drag, swimmers attempt to make contact surfaces as smooth as possible by wearing swim caps and shaving their legs. Likewise, an aircraft's wing is designed to be smooth to reduce drag.

Like lift, drag is proportional to dynamic pressure and the area on which it acts. The drag coefficient, analgous to the lift coefficent, is a measure of the amount of dynamic pressure gets converted into drag. Unlike the lift coefficient however, engineers usually design the drag coefficient to be as low as possible. Low drag coefficients are desirable because an aircraft's efficiency increases as drag decreases.

Weight

The weight of an aircraft is a limiting factor in aircraft design. A heavy plane, or a plane meant to carry heavy payloads, requires more lift than a light plane. It may also require more thrust to accelerate on the ground. On small aircraft the location of weight is also important. A small plane must be appropriately "balanced" for flight, for too much weight in the back or front can render the plane unstable. Weight can be calculated using a form of Newton's second law:

W = mg

where W is weight, m is mass, and g is the acceleration due to gravity on Earth.

Thrust

Propulsion involves a number of principles of physical science. Thermodynamics, aerodynamics, fluid mathematics, and physics all play a role. Thrust itself is a force than can best be described by Newton's second law. The basic form of this law is:

F = ma

which states that force (F) is equal to mass (m) times acceleration (a). Acceleration is the rate of change of velocity over time. Thrust (T) is produced therefore by accelerating a mass of air.

Class Discussion

  1. Would more lift be provided by a fluid with a greater density than air?
  2. How do aircraft designers determine the correct shape for a wing?
  3. Explain how a propeller provides thrust in the same way a wing generates lift.
  4. An equation for lift was supplied previously. What would be the two forces involved on a propeller?
  5. Would a propeller work better in a fluid with a greater density than air?
  6. Do you think different planes need differently shaped airfoils?
  7. During the design phase, how is a wing's theoretical shape tested?
  8. How are the wings of a small plane, like a Cessna, different from a large one, like a passenger jet?
  9. How are the propulsion systems of a biplane different than that of a fighter jet?
  10. What kind of propulsion does a Lear jet use? The Concorde?
  11. Make a list of the differences between fixed wing aircraft and helicopters. How does each generate lift? How fast can each go? What are the advantages and disadvantages of each?
  12. Some planes have more than one engine to propel the craft. Are the multiple engines necessary or a safety precaution?

Class Activities/Research

  1. Build paper airplanes and demonstrate the effects of lift, drag, thrust, and weight.
  2. Take a trip to your local airport or an airshow. Visit the control tower and the aircraft hangers.
  3. Determine the wing area of a large aircraft. Describe what kind of plane it is.
  4. What kind of propulsion system does the space shuttle use, as opposed to an airplane?
  5. Who are the leading manufacturers of aircraft engines?

Problems

  1. Derive the basic equation for lift (Eqn 3) from Bernoulli's Equation (Eqn 1). Note any assumptions that you make.
  2. What is the density of air? Does it differ from high altitudes to low altitudes?
  3. Draw a free-body diagram of an aircraft.

Man-Vehicle Laboratory
MIT Department of Aeronautics and Astronautics
sablan@mit.edu
16 March 1997