Viscous Aerodynamic Analysis -- Asymptotic Approach

Viscous Aerodynamic Analysis -- Asymptotic Approach Viscous Aerodynamic Analysis - Asymptotic Approach

1 Governing equations

The typical steady incompressible viscous aerodynamic analysis problem is to determine the velocity field u = (u,v) and pressure field p about a specified geometry. The governing Navier-Stokes Equations are solved together with the appropriate boundary conditions.

Ñ·u

u ·Ñu

-Ñp + e² Ñ² u

b.c. in freestream:

u = u_¥

b.c. on body:

u =

®
0

(1)

Using standard Dimensional Analysis, the variables have been normalized with some reference velocity u_ref, reference length l_ref, reference pressure ru_ref². The associated reference Reynolds number has been recast as a parameter

e º Re^-1/2 = (u_ref l_ref / n)^-1/2

with Re >> 1 and hence e << 1 being characteristic of most practical aerodynamic problems. Example values based on the freestream velocity and wing chord reference quantities are:

device Re e
model airplane 1 ×10⁴-5 ×10⁵ 0.01 - 0.0015
light aircraft 1 ×10⁶-5 ×10⁶ 0.001 - 0.0005
heavy aircraft 5 ×10⁶-5 ×10⁷ 0.0005 - 0.00015

2 Inner-Outer Domains

Examination of equations (1) reveals that because of the no-slip condition, the convective term u ·Ñu is zero at a solid boundary. Consequently, even when e becomes vanishingly small, the highest-order viscous term e² Ñ² u must remain finite at a solid boundary since it alone remains to provide a Dominant Balance with the nonzero pressure gradient term Ñp.

Near wall: e² Ñ² u = Ñp = O(1)

Hence, Ñ² u must be O(1/e²), and therefore the derivatives of u will become singular near solid boundaries in the limit of vanishing e. To obtain a non-singular solution, two separate sets of variables and equations are used - one set for the viscous shear layers, and a second set for the remaining outer flow, as shown in Figure 1. For the outer flow, the solution is well-behaved and the original flow variables u,v are retained. For the inner flow description, the singularity is removed by suitably rescaling the vertical coordinate and vertical velocity variables with e.

X = x

Y = y/e

U = u

V = v/e

(2)

The equations of the outer flow are the same as (1), except that the wall boundary condition is replaced by a matching condition with the inner flow.

Ñ·u

u ·Ñu

-Ñp + e² Ñ² u

b.c. in freestream:

u = u_¥

b.c. at edge:

u = (U , eV)

(3)

The equations for the inner flow are likewise obtained from (1), with the freestream boundary condition replaced by a matching condition with the outer flow at the edge of the inner region.

¶U

¶X

¶V

¶Y

¶U

¶X

+ V

¶U

¶Y

¶p

¶X

+ e²

æ
ç
è

¶² U

¶X²

e²

¶² U

¶Y²

ö
÷
ø

¶V

¶X

+ V

¶V

¶Y

e²

¶p

¶Y

+ e²

æ
ç
è

¶² V

¶X²

e²

¶² V

¶Y²

ö
÷
ø

b.c. at edge:

(U,V) = (u , v/e)

b.c. on body:

(U,V) = (0,0)

(4)

Figure 1: Inner and outer flowfield domains.

3 Asymptotic expansions

The typically small values of the parameter e suggest writing the sought-after solution as a Matched Asymptotic Expansion

u(x,y ; e)

u₀(x,y) + e u₁(x,y) + e² u₂(x,y) + ¼

p(x,y ; e)

p₀(x,y) + e p₁(x,y) + e² p₂(x,y) + ¼

U(X,Y ; e)

U₀(X,Y) + e U₁(X,Y) + e² U₂(X,Y) + ¼

V(X,Y ; e)

V₀(X,Y) + e V₁(X,Y) + e² V₂(X,Y) + ¼

(5)

which simplifies the potentially complex dependence on e to a polynomial form. Only a few leading terms should suffice owing to the very small magnitude of e. The expansions (5) can now be substituted into the governing equations (1) and the terms grouped into powers of e.

3.1 Zeroth-order equations (Classical Theory)

The zeroth-order equations for the outer domain, with all powers of e neglected, are

Ñ·u

u ·Ñu

-Ñp

in freestream:

u = u_¥

at edge:

v = 0

(6)

which are simply the equations for inviscid flow, except that the no-slip vector boundary condition has been reduced to the zero normal velocity (or flow-tangency) scalar condition. The condition on the tangential velocity has had to be dropped to accomodate the reduction of the order of the equations when the viscous term was neglected.

The zeroth-order equations for the inner domain are

¶U

¶X

¶V

¶Y

¶U

¶X

+ V

¶U

¶Y

¶p

¶X

¶² U

¶Y²

¶p

¶Y

at edge:

U = u

on body:

(U,V) = (0,0)

(7)

The outer boundary condition is imposed only on the tangential velocity U (taken from u in the outer domain). The reduction of order in the equations has required the elimination of the outer boundary condition on V, this now being a result of the solution. The pressure p is also taken from the outer domain, typically via the Bernoulli relation

p = const -

u² ® -

¶p

¶X

= u

¶u

¶x

with the v terms dropped up to the first-order approximations.

The overall zeroth-order equation system (6) and (7) constitutes the Classical Boundary Layer Theory problem. It has the following features:

The outer domain equations correspond to inviscid flow. They are most conveniently solved by introduction of the zeroth-order Velocity Potential f(x,y).
The inner domain equations correspond to the classical Thin Shear Layer Equations. They can be further transformed to eliminate singularities at leading edges, such as the Local Scaling Transformation, or its subset the Falkner-Skan Transformation.
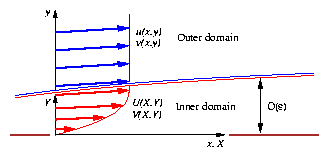
There is a one-way coupling from the outer to the inner equations: The outer equations can be solved first independently, and the resulting velocity u then provides the boundary condition and pressure-gradient term for the inner equations, as shown in Figure 2.

3.2 First-order equations (Interacting Boundary Layer Theory)

The first-order equations for the outer domain, with powers of e² and higher neglected, are

Ñ·u

u ·Ñu

-Ñp

in freestream:

u = u_¥

at edge:

v = e V

(8)

which again are the equations for inviscid flow, but the imposed normal velocity at the matching point is now nonzero, and is obtained from the inner domain.

The first-order equations for the inner domain are

¶U

¶X

¶V

¶Y

¶U

¶X

+ V

¶U

¶Y

¶p

¶X

¶² U

¶Y²

¶p

¶Y

at edge:

U = u

on body:

(U,V) = (0,0)

(9)

These are identical to the zeroth-order equations, except that the imposed tangential velocity u of the outer domain will now be different from the zeroth-order case due to its modified normal-velocity boundary condition.

The overall first-order equation system (8) and (9) constitutes the Intaractive Boundary Layer Theory problem. It has the following features:

The outer domain equations still correspond to inviscid flow, which is still treatable using the velocity potential. The modified flow-tangency boundary condition can be imposed using one of several Boundary Layer Interaction Models.
The inner domain equations still correspond to the classical Thin Shear Layer Equations, and are treatable with the usual transformation methods.
There is now a two-way coupling between the outer and the inner equations, making all equations one fully-coupled system as shown in Figure 2.

Figure 2: Classical and IBLT viscous analysis treatments.

device	Re	e
model airplane	1 ×10⁴-5 ×10⁵	0.01 - 0.0015
light aircraft	1 ×10⁶-5 ×10⁶	0.001 - 0.0005
heavy aircraft	5 ×10⁶-5 ×10⁷	0.0005 - 0.00015