1  Definitions

The details of the velocity profile u(y) at any x location are rarely significant in engineering applications. The most significant quantities are integral thicknesses which describe the mass flux, momentum flux, and kinetic energy flux in the shear layer:

2  Integral Thickness Interpretation

These thicknesses appear when comparing the mass, momentum, and kinetic energy flows in a shear layer and a corresponding potential flow.

2.1  Mass flow comparison

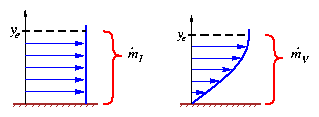
Figure shows the mass flux passing between the vertical extent y = 0 ¼y_e for inviscid and viscous flows with the same edge velocity.

2.2  Momentum flow comparison

Figure shows the momentum flux carried by the mass flow passing between y = 0 ¼y_e of the inviscid case. The viscous case capture height is increased by d^* so that the comparison is done at the same mass flows. In each case, the momentum flow can be considered to be the force acting on a barrier which arrests the flow velocity to zero.

2.3  Kinetic energy flow comparison

Figure shows the kinetic energy flux carried by the mass flow passing between y = 0 ¼y_e of the inviscid case. The viscous case capture height is again increased by d^* so that the comparison is done at the same mass flows. In each case, the kinetic energy flow can be considered to be the power generated on an array of perfect windmills which reversibly bring the flow velocity to zero.

mom