1  Potential Flow Perturbation

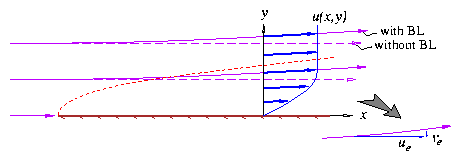
Asymptotic analysis of the Viscous Aerodynamic Problem indicates that the boundary layer perturbs the potential flow via the displacement effect by an amount which is O(Re^-1/2). This perturbation may be important when high prediction accuracy is required for aerodynamic quantities such as lift and drag. For separated flow the perturbation to the potential flow can be O(1), and accounting for the perturbation is essential.

Two common methods are formualted here to modify the potential flow problem to account for the boundary layer's presence. Each method is constructed so as to match the vertical velocity v_e of the actual flow just outside the viscous region.

2  Actual Flow

The actual flow situation is shown in Figure .

The vertical velocity at some location y_e is computed in terms of the mass defect gradient via the continuity equation.

3  Displacement Body Model

This model employ the concept of a fictitious displacement body, which is offset from the actual body by a distance D(x).

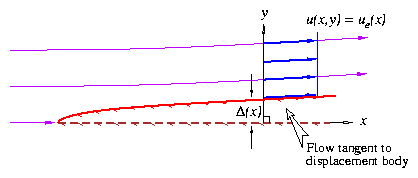
The displacement body is assumed to have a purely potential flow tangent to it. The resulting v_e in this situation is again computed using the continuity equation.

4  Wall Blowing Model

This model employs the actual body shape, but defines a fictitious wall blowing distribution v_wall(x).

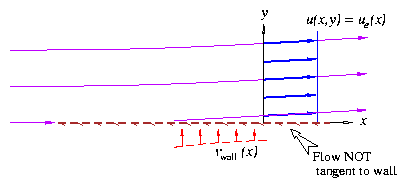
The flow is assumed to be purely potential, but it is not tangent to the actual body because of v_wall(x) ¹ 0. The resulting v_e at some distance above the wall follows from continuity.