Handed Out: 2/5/98
Due: 2/12/98
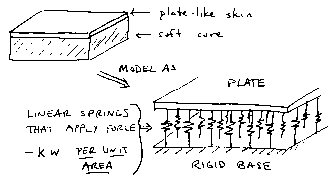
1. Consider a structure consisting of a relatively stiff skin of material covering a soft core. This type of construction is used for many purposes, from insulated building panels to light aircraft wings. We wish to develop plate-like equations to describe the response of the skin to lateral loading. The soft core does not help very much, but it does resist lateral loadings by pushing back linearly, so we will model it as if it consisted of linear springs (see below).

a) Develop the equilibrium equations for an element of the skin.
b) Using the strain displacement and stress-strain equations developed in class, reduce the results of part a) to a single governing equation in bending, and two in-plane. Show that the core (at least as modeled above) has no effect on the in-plane response.
2. Now consider a real structure's B.C.'s. Unfortunately, they tend to be hard to put in the categories that are mathematically simple- clamped, pinned, etc. Develop mathematical expressions for the "general" boundary conditions shown below, and show that they reduce to idealized boundary conditions in the limits of k = 0 and k = infinity
 .
.