Handed Out: 2/26/98
Due: 3/5/98
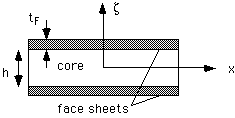
1. Use the definition of the M's and the assumption of linearly varying strain through the thickness to find the axial stress sigma(x) as a function of position through the thickness zeta for the sandwich panel shown below. Make simplifying assumptions as necessary; state them. Then use equilibrium, the moment-shear force relation, and the boundary condition that there is no shear stress on the top and bottom of the plate to find the out-of-plane shear stress tau(xz) as a function of zeta. Assume the moments and shear forces are known.

2. A simple supported square plate 24" on a side is loaded with a constant side load of 5 psi. Find the maximum deflection, inplane stress, and shear stress, and any interesting behavior, for the following constructions. Use any theories, assumptions, etc. you find appropriate.
3. It is proposed that for certain classes of orthotropic plates we can save a lot of bother by using the following method. If we have an isotropic plate a x b, simply supported on all sides, with stiffness D, under a constant load pz, we can easily find a solution that we can express (in dimensionless form) as w(x/a, y/b) Consider and orthotropic plate a' x b', with stiffnesses D11, D22, D12 , and D66, and loading pz'. Set D11= D for convenience. For a given D22= c*D11 (where c is an arbitrary constant) can you find a set of a', b', pz', D12 and D66 such that the solution to the orthotropic problem w' when expressed in dimensionless form w'(x'/a', y'/b') is the same as w(x/a, y/b)? Try plugging a one-mode Navier solution into the isotropic and orthotropic governing equations. Then try to find a' and b' as functions of a, b, and c, and determine if there are any special condition on D12 and D66, in order to get w' = w. Does this work? If not, why? If so, will it generalize to the higher modes?