Handed Out: 3/12/98
Due: 3/19/98
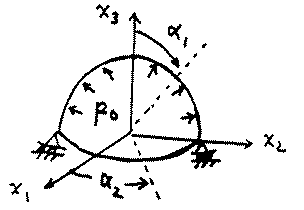
1. A hemispherical shell of radius R is loaded by an internal pressure po. Using membrane theory, find the stress resultants N1, N2 and the deflections u1, w. Note A1 = R, A2 = Rsin(alpha1), R1 = R, and R2 = R in this case.

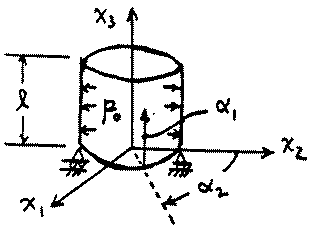
2. A sylindrical shell of radius R is loaded by an internal pressure po. The end alpha1 = small-L is free to expand in the x3 direction. Using membrane theory, find the stress resultants N1, N2 and the deflections u1, w. Note A1 = 1, A2 = R, R1 = infinity, and R2 = R in this case, and the boundary conditions at alpha1 = small-L are N1 = Force/Circumference = po*pi*R^2/(2*pi*R)
3. A pressure vessel is constructed of a cylinder with hemispherical end caps. Will pure membrane theory be sufficient to analyze this structure? What is the problem?
4. Check out Sheplak, M., and Dugundji, J., "Large Deflections of Clamped Circular Plates Under Initial Tension and Transitions to Membrane Behavior," J. Applied Mechanics, Vol. 65, March 1998. Solve the extreme cases-the plate and membrane solutions-and check your answers for w/wo(x) against those of Sheplak and Dugundji.