Thermodynamics and Propulsion

3.1 Some Properties of Engineering Cycles; Work and Efficiency

As preparation for our discussion of cycles (and as a foreshadowing of the second law), we examine two types of processes that concern interactions between heat and work. The first of these represents the conversion of work into heat. The second, which is much more useful, concerns the conversion of heat into work. The question we will pose is how efficient can this conversion be in the two cases.

Figure 3.1: Examples of the conversion of work into heat

Three examples of the first process are given in Figure 3.1. The first is the pulling of a block on a rough horizontal surface by a force which moves through some distance. Friction resists the pulling. After the force has moved through the distance, it is removed. The block then has no kinetic energy and the same potential energy it had when the force started to act. If we measured the temperature of the block and the surface we would find that it was higher than when we started. (High temperatures can be reached if the velocities of pulling are high; this is the basis of inertia welding.) The work done to move the block has been converted totally to heat.

The second example concerns the stirring of a viscous liquid. There is work associated with the torque exerted on the shaft turning through an angle. When the stirring stops, the fluid comes to rest and there is (again) no change in kinetic or potential energy from the initial state. The fluid and the paddle wheels will be found to be hotter than when we started, however.

The final example is the passage of a current through a resistance. This is a case of electrical work being converted to heat, indeed it models operation of an electrical heater.

All the examples in Figure 3.1 have 100% conversion of work into heat. This 100% conversion could go on without limit as long as work were supplied. Is this true for the conversion of heat into work?

To answer the last question, we need to have some basis for judging whether work is done in a given process. One way to do this is to ask whether we can construct a way that the process could result in the raising of a weight in a gravitational field. If so, we can say ``Work has been done.'' It may sometimes be difficult to make the link between a complicated thermodynamic process and the simple raising of a weight, but this is a rigorous test for the existence of work.

One example of a process in which heat is converted to work is the isothermal (constant temperature) expansion of an ideal gas, as sketched in Figure 3.2. The system is the gas inside the chamber. As the gas expands, the piston does work on some external device. For an ideal gas, the internal energy is a function of temperature only, so that if the temperature is constant for some process the internal energy change is zero. To keep the temperature constant during the expansion, heat must be supplied. Because $\Delta U = 0,$ the first law takes the form $Q=W$ . This is a process that has 100% conversion of heat into work.

Figure 3.2: Isothermal expansion

The work exerted by the system is given by

$$\textrm{Work} =\int_1^2 PdV$$

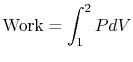
where 1 and 2 denote the two states at the beginning and end of the process. The equation of state for an ideal gas is

$$P = N\mathcal{R}T/V,$$

with $N$ the number of moles of the gas contained in the chamber. Using the equation of state, the expression for work can be written as

$$\textrm{Work during an isothermal expansion }= N\mathcal{R}T \int_1^2 dV/V = N\mathcal{R}T \ln\left(\frac{V_2}{V_1}\right).$$ (3..1)

For an isothermal process, $PV = \textrm{constant}$ , so that ${P_1}/{P_2} = {V_2}/{V_1}$ . The work can be written in terms of the pressures at the beginning and end as

$$\textrm{Work during an isothermal expansion }= N\mathcal{R}T \ln\left(\frac{P_1}{P_2}\right).$$ (3..2)

The lowest pressure to which we can expand and still receive work from the system is atmospheric pressure. Below this, we would have to do work on the system to pull the piston out further. There is thus a bound on the amount of work that can be obtained in the isothermal expansion; we cannot continue indefinitely. For a power or propulsion system, however, we would like a source of continuous power, in other words a device that would give power or propulsion as long as fuel was added to it. To do this, we need a series of processes where the system does not progress through a one-way transition from an initial state to a different final state, but rather cycles back to the initial state. What is looked for is in fact a thermodynamic cycle for the system.

We define several quantities for a cycle:

• $Q_A$ is the heat absorbed by the system.
• $Q_R$ is the heat rejected by the system.
• $W$ is the net work done by the system.

The cycle returns to its initial state, so the overall energy change, $\Delta U$ , is zero. The net work done by the system is related to the magnitudes of the heat absorbed and the heat rejected by

$$W = \textrm{Net work} = Q_A -Q_R.$$

The thermal efficiency of the cycle is the ratio of the work done to the heat absorbed. (Efficiencies are often usefully portrayed as ``What you get'' versus ``What you pay for.'' Here what we get is work and what we pay for is heat, or rather the fuel that generates the heat.) In terms of the heat absorbed and rejected, the thermal efficiency is

$$\eta = \textrm{thermal efficiency} = \frac{\textrm{Work done}}{\textrm{Heat absorbed}} =\frac{Q_A-Q_R}{Q_A}=1-\frac{Q_R}{Q_A}.$$ (3..3)

The thermal efficiency can only be 100% (complete conversion of heat into work) if $Q_R=0$ ; a basic question is what is the maximum thermal efficiency for any arbitrary cycle? We examine this for several cases, including the Carnot cycle and the Brayton (or Joule) cycle, which is a model for the power cycle in a jet engine.