|
[VW, S & B: 6.3-6.4]
Reversible processes are idealizations or models of real processes.
One familiar and widely used example is Bernoulli's equation, which
you saw in Unified. They are extremely useful for defining limits to
system or device behavior, for enabling identification of areas in
which inefficiencies occur, and in giving targets for design.
An important feature of a reversible process is that, depending on
the process, it represents the maximum work that can be extracted in
going from one state to another, or the minimum work that is needed
to create the state change.
Let us consider processes that do work, so that we can show that the
reversible one produces the maximum work of all possible
processes between two states. For example, suppose we have a
thermally insulated cylinder that holds an ideal gas,
Figure 4.9. The gas is contained by a thermally
insulated massless piston with a stack of many small weights on top
of it. Initially the system is in mechanical and thermal
equilibrium.
Figure 4.9:
A piston with weights on top
|
|
Consider the following three processes, shown in
Figure 4.10:
- All of the weights are removed from
the piston instantaneously and the gas expands until its volume is
increased by a factor of four (a free expansion).
- Half of the
weight is removed from the piston instantaneously, the system is
allowed to double in volume, and then the remaining half of the
weight is instantaneously removed from the piston and the gas is
allowed to expand until its volume is again doubled.
- Each small
weight is removed from the piston one at a time, so that the
pressure inside the cylinder is always in equilibrium with the
weight on top of the piston. When the last weight is removed, the
volume has increased by a factor of four.
Figure 4.10:
Getting the most work out of a system requires that
the work be extracted reversibly
|
|
Maximum work (proportional to the area under these curves) is
obtained for the quasi-static expansion.
To reiterate:
- The work done by a system during a reversible process is the maximum
work we can get.
- The work done on a system in a reversible
process is the minimum work we need to do to achieve that state
change.
A process must be quasi-static (quasi-equilibrium) to be reversible.
This means that the following effects must be absent or
negligible:
- Friction: If
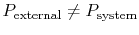 we
would have to do net work to bring the system from one volume to
another and return it to the initial condition (recall
Section 1.3.3.)
we
would have to do net work to bring the system from one volume to
another and return it to the initial condition (recall
Section 1.3.3.)
- Free (unrestrained) expansion.
- Heat transfer through a finite temperature
difference.
Figure 4.11:
Heat transfer across a finite
temperature difference
|
|
Suppose we have heat transfer from a high temperature to a lower
temperature as shown in Figure 4.11. How do we
restore the situation to the initial conditions? One thought would
be to run a Carnot refrigerator to get an amount of heat, 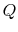 , from
the lower temperature reservoir to the higher temperature reservoir.
We could do this but the surroundings, again us, would need to
provide some amount of work (which we could find using our analysis
of the Carnot refrigerator). The net (and only) result at the end of
the combined process would be a conversion of an amount of work into
heat. For reversible heat transfer from a heat reservoir to a
system, the temperatures of the system and the reservoir must be
, from
the lower temperature reservoir to the higher temperature reservoir.
We could do this but the surroundings, again us, would need to
provide some amount of work (which we could find using our analysis
of the Carnot refrigerator). The net (and only) result at the end of
the combined process would be a conversion of an amount of work into
heat. For reversible heat transfer from a heat reservoir to a
system, the temperatures of the system and the reservoir must be
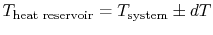 . In other
words the difference between the temperatures of the two entities
involved in the heat transfer process can only differ by an
infinitesimal amount,
. In other
words the difference between the temperatures of the two entities
involved in the heat transfer process can only differ by an
infinitesimal amount, 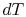 .
.
While all natural processes are irreversible to some extent, it
cannot be emphasized too strongly that there are a number of
engineering situations where the effect of irreversibility can be
neglected and the reversible process furnishes an excellent
approximation to reality.
The second law, which is the next topic we address, allows us to
make a quantitative statement concerning the irreversibility of a
given physical process.
Figure 4.12:
Nicolas Sadi Carnot (1796-1832), an
engineer and an officer in the French army. Carnot's work is all the
more remarkable because it was made without the benefit of either the
first or second law. The second law was not discovered until 30 years
later. [Atkins, The Second Law]
|
|
Muddy Points
Is heat transfer across a finite temperature difference only
irreversible if no device is present between the two to harvest the
potential difference?
(MP 4.5)
UnifiedTP
| 
