|
Reynolds and Perkins give a numerical example which illustrates the
above concepts and also the tendency of a closed isolated system to
tend to equilibrium. The starting point is a system in an initial
microscopic state that is not an equilibrium distribution. We expect
the system will change quantum state, with disorder, randomness
growing until they reach the equilibrium values. The specific system
to be studied is composed of 10 particles 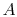 ,
, 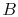 ,
, 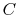 , ...,
, ..., 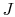 ,
each of which can exist in one of 5 states, of energies 0, 1, 2, 3,
4. The system is isolated and has a total energy of 30. The total
energy remains unchanged during the evolution of the microscopic
states. Some of the allowed states are shown in
Figure 7.1
,
each of which can exist in one of 5 states, of energies 0, 1, 2, 3,
4. The system is isolated and has a total energy of 30. The total
energy remains unchanged during the evolution of the microscopic
states. Some of the allowed states are shown in
Figure 7.1
Figure 7.1:
Some allowed states of the system
in the numerical example. Note each state has a total energy of 30.
[Reynolds and Perkins, 1977]
|
|
Figure 7.2:
Constant energy state groups [Reynolds
and Perkins, 1977]
|
|
For ten particles, 4 energy states, and a total energy of 30, there
are 72,403 possible quantum states (4 states are indicated in
Figure 7.1). However, there are only 23
possible distributions in terms of the number of particles having a
given energy as shown in
Figure 7.2. For example, states 2
and 3 in Figure 7.1 are two different quantum
states, but they represent the same group (22) in
Figure 7.2. The allowed state
groups
If the quantum-state probabilities are equal, each quantum state has
a probability of 1/72,403. The probabilities of each group are thus
directly proportional to the number of quantum states in this group.
For instance, group 22 has 90 quantum states, so its probability is
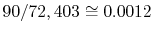 . We now know what the equilibrium
distribution of probabilities is. We now address the time evolution
of a system to the equilibrium state. To see this, we start a system
from one of the 22 non-equilibrium groups and track the behavior
over time. A way to examine the process is to consider what happens
if two particles interact, doing this numerically for the
instantaneous quantum state. The two particles are free to change
energy as long as the total energy of the system is conserved. This
may or may not end up by changing the state group (the particles
could interact and only switch states). There are 45 possible pairs
for this interaction (there are
. We now know what the equilibrium
distribution of probabilities is. We now address the time evolution
of a system to the equilibrium state. To see this, we start a system
from one of the 22 non-equilibrium groups and track the behavior
over time. A way to examine the process is to consider what happens
if two particles interact, doing this numerically for the
instantaneous quantum state. The two particles are free to change
energy as long as the total energy of the system is conserved. This
may or may not end up by changing the state group (the particles
could interact and only switch states). There are 45 possible pairs
for this interaction (there are
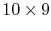 possible ways to carry
out the interaction, but two of them, say interactions between
possible ways to carry
out the interaction, but two of them, say interactions between  and
and  and
and 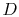 and
and 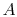 , are the same), and we assume that any of
them is equally likely to happen.
, are the same), and we assume that any of
them is equally likely to happen.
If the system is initially in state 1 of
Figure 7.1, it is in group 23 of
Figure 7.2. For each of the 45
pairs, there are two interactions that take the system to group 22,
and one that leaves the system unchanged. (For interactions between
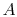 and
and 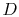 , say, the result can be that
, say, the result can be that 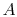 and
and 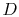 have their
energy unchanged, that
have their
energy unchanged, that 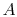 loses energy and
loses energy and 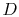 gains energy, or
that
gains energy, or
that 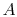 gains energy and
gains energy and 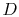 loses energy. In the first of these,
the system will remain in group 23. In the second and third it will
move to group 22.) Hence the transition probability from
group 23 to group 22 is
loses energy. In the first of these,
the system will remain in group 23. In the second and third it will
move to group 22.) Hence the transition probability from
group 23 to group 22 is 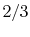 , and the transition probability from
23 to 23 is
, and the transition probability from
23 to 23 is 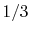 .
.
Figure 7.3:
Transition probabilities
(probability for transition from initial group to final group) in
numerical experiment with isolated system [Reynolds and Perkins,
1977]
|
|
For the other groups, the transitions are more complicated, but can
be found numerically, with the results shown in
Figure 7.3. The numerical experiments
were carried out with the system initially in state 23 and with
successive interactions chosen randomly in accordance with the
transition probabilities of
Figure 7.3. The experiment was
repeated 10,000 times, with a different group history traced out
each time and, again, the system energy maintained at 30. The
fraction of the experiments in which each group occurred at time 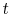 was used to calculate the group probabilities
was used to calculate the group probabilities 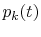 at each time.
The entropy was then found for the distribution
at each time.
The entropy was then found for the distribution 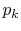 at that time.
at that time.
Figure 7.4:
Evolution of the
probability distribution with time (interaction number) [Reynolds
and Perkins, 1977]
|
|
Figure 7.4 shows the evolution
of some of the 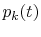 with time (the unit of time is the
interaction number for the calculations) starting from group 23.
After roughly ten interactions, the probabilities have reached a
steady-state level, which are the equilibrium probabilities from
Figure 7.2.
with time (the unit of time is the
interaction number for the calculations) starting from group 23.
After roughly ten interactions, the probabilities have reached a
steady-state level, which are the equilibrium probabilities from
Figure 7.2.
Figure 7.5:
Entropy for the system as a
function of time [Reynolds and Perkins, 1977]
|
|
The computed entropy is given in Figure 7.5
as a function of time. It increases to the equilibrium value with
the same sort of behavior as the probability distribution.
The interactions allow the system to change groups. The transition probabilities are large for
groups with high equilibrium probabilities.
There is one additional aspect of the behavior that is brought out
in the text. This is the difference in overall probabilities between
the order of transitions. The probability of a transition sequence
is the product of the individual step transition probabilities. The
transition 23-22-12-9-1 thus has the probability:
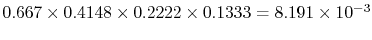 . The
reverse transition, 1-9-12-22-23 has the probability:
. The
reverse transition, 1-9-12-22-23 has the probability:
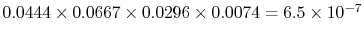 . There is an enormous
probability that the system will move towards (and persist in)
quantum state groups that have high equilibrium probabilities. Once
a system has moved out of group 23, there is little likelihood that
it will ever return. Further, for engineering systems, which have
not 10 particles, but upwards of
. There is an enormous
probability that the system will move towards (and persist in)
quantum state groups that have high equilibrium probabilities. Once
a system has moved out of group 23, there is little likelihood that
it will ever return. Further, for engineering systems, which have
not 10 particles, but upwards of 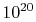 , the difference between
transitions and their reverses are much more marked, and the
probability is overwhelming that the distribution will be a quantum
state with a broad distribution of particle energies.
, the difference between
transitions and their reverses are much more marked, and the
probability is overwhelming that the distribution will be a quantum
state with a broad distribution of particle energies.
UnifiedTP
|

