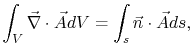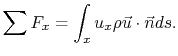|
Consider two coordinate systems:
- Inertial (labeled with subscript
 in
Figure 10.1),
in
Figure 10.1),
- Fixed to vehicle (labeled with subscript
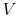 in
Figure 10.1)
in
Figure 10.1)
- Moves with velocity
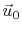 relative to the
inertial coordinate system.
relative to the
inertial coordinate system.
- All velocities relative to the
vehicle-fixed coordinate frame are denoted
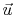 .
.
Figure 10.1:
Two inertial coordinate systems, one stationary, one translating
|
|
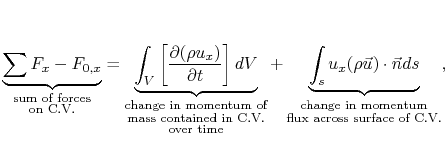
Newton's second law for a control volume of fixed mass can be
written as
or
where the external forces acting on the control volume may be
pressures forces, shear forces (skin friction), and body forces.
To explain the above equation further, consider
Figure 10.2.
Figure 10.2:
Falling blocks
|
|
The falling block labeled (a) has a control volume fixed to it. In
this case, the first term of the above equation is nonzero since the
control volume is accelerating relative to an inertial reference
frame. The second term is zero because the block is not accelerating
relative to a coordinate system fixed to the control volume. The
opposite is true for the falling block labeled (b), which is falling
within a fixed control volume. The first term of the above equation
is zero in this case because the control volume is not accelerating
relative to an inertial reference frame. The second term is nonzero
because the block is moving to a coordinate system fixed to the
control volume. The mathematical result of both cases is as follows:
-
-
As expected, the result is the same for
both. The integral momentum equation reduces to a familiar form,
 . To
continue, the integral momentum equation can be rewritten as
follows,
. To
continue, the integral momentum equation can be rewritten as
follows,
From conservation of mass,
so
Note that this is a vector equation. Considering only the
components in the 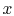 -direction
-direction
Then, by the
divergence theorem,
where 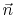 is outward unit normal vector. We thus have
is outward unit normal vector. We thus have
where again the forces acting on the control volume may be composed
of pressure forces, body forces, and skin friction.
For steady flow, with no acceleration of the vehicle then
This is the form we will use most frequently in
this class.
UnifiedTP
|


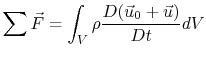
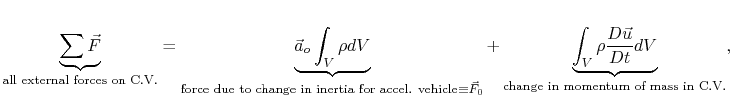
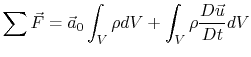
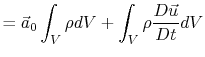
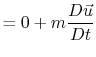
![$\displaystyle = \int_V \rho\left[\frac{\partial\vec{u}}{\partial t} + \vec{u}\vec{\nabla}\vec{u}\right]dV$](img1217.png)
![$\displaystyle =\int_V\left[\rho\frac{\partial \vec{u}}{\partial t} + \vec{u}\fr...
...u}\frac{\partial \rho}{\partial t}+\rho\vec{u}\cdot\vec{\nabla}\vec{u}\right]dV$](img1218.png)
![$\displaystyle =\int_V\left[\frac{\partial(\rho \vec{u})}{\partial t} -\vec{u}\frac{\partial \rho}{\partial t}+\rho\vec{u}\cdot\vec{\nabla}\vec{u}\right]dV.$](img1219.png)
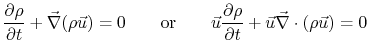
![$\displaystyle \sum\vec{F}-\vec{F}_0=\int_V\left[\frac{\partial(\rho\vec{u})}{\p...
...c{u}\vec{\nabla}\cdot(\rho\vec{u})+\rho\vec{u}\cdot\vec{\nabla}\vec{u}\right]dV$](img1221.png)
![\begin{displaymath}\begin{split}\sum F_x-F_{0,x} &= \int_V\left[\frac{\partial(\...
...x)}{d t}+\vec{\nabla}\cdot(\rho u_u \vec{u})\right] \end{split}\end{displaymath}](img1222.png)