

|
|
| Thermodynamics and Propulsion | |
11.8 Muddiest points on Chapter 11
MP 11..1
What exactly is the specific impulse,
The specific impulse is a measure of how well the fuel is used in
creating thrust. For a rocket engine, the specific impulse is the
effective exit velocity divided by the acceleration of gravity,
From this, one can regard the specific impulse as the time that it would take to flow a quantity of fuel that has a weight equal to the thrust force.
MP 11..2
How is
The impulse
MP 11..3
Why does industry use
I am not sure why Thrust Specific Fuel Consumption was originally
used. The gas turbine industry uses
MP 11..4
Why isn't mechanical efficiency an issue with ramjets?
As defined, the mechanical efficiency represents bearing friction, and other parasitic torques on the rotating shaft in a gas turbine. The work associated with this needs to be provided by the turbine, but does not go into driving the compressor. The ramjet has no shaft, and hence does not encounter this.
MP 11..5
How is thrust created in a ramjet?
You can look at thrust in several ways. One is through the integral form of the momentum equation, which relates thrust to the difference between exit and inlet velocities, multiplied by the mass flow. Another way, however, is to look at the forces on the ramjet structure, basically the summation of pressure forces on all the surfaces. I attempted to do this in class using the turbojet with an afterburner. For the ramjet, from the same considerations, we would have an exit nozzle that was larger in diameter than the inlet so that the structural area on which there is a force in the retarding direction is smaller than the area on which there is a force in the thrust direction.
MP 11..6
What is the relation between
The two are very different physical statements. The first is the
SFEE (steady flow energy equation) plus the approximation that inlet
and exit mass flows to the control volume are the same. The heat
received within the volume is represented by the quantity
MP 11..7
Why didn't we have a 2s point for the Brayton cycle with
non-ideal components?
If we didn't, we should have, or I should at least have marked the point at which the compressor exit would be if the compression process was isentropic.
MP 11..8
What is the variable
MP 11..9
Isn't it possible for the mixing of two gases to go from the
final state to the initial state? If you have two gases in a box,
they should eventually separate by density, right?
Let us assume that gas
MP 11..10
How can
I agree that the
MP 11..11
When there are losses in the turbine that shift the
expansion in
We have to be careful when looking at the area enclosed by a cycle
or underneath a path in the
MP 11..12
For an afterburning engine, why must the nozzle throat area
increase if the temperature of the fluid is increased?
The Mach number of the flow is unity at the throat with and without the afterburner lit. The ratio of static pressure to stagnation pressure at the throat is thus the same with and without the afterburner lit. The ratio of static temperature to stagnation temperature at the throat is thus the same with and without the afterburner lit.
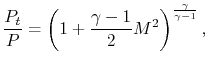
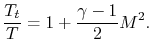
The flow through the throat is

The flow through the throat thus scales as
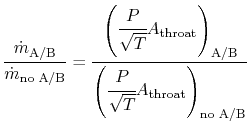
From what we have said, however, the pressure at the throat is the same in both cases. Also, we wish to have the mass flow the same in both cases in order to have the engine operate at near design conditions. Putting these all together, plus use of the idea that the ratio of stagnation to static temperature at the throat is the same for both cases gives the relation
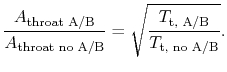
The necessary area to pass the flow is proportional to the square root of the stagnation temperature. If too much fuel is put into the afterburner, the increase in area cannot be met and the flow will decrease. This can stall the engine, a serious consequence for a single engine fighter.
MP 11..13
Why doesn't the pressure in the afterburner go up if heat is
added?
From discussions after lecture, the main point here seems to be that
the process of heat addition in the afterburner, or the combustor,
is not the same as heat addition to a gas in a box. In that case the
density (mass/volume) would be constant and, from
MP 11..14
Why is the flow in the nozzle choked?
As seen in Unified, choking occurs when the stagnation to static
pressure ratio
MP 11..15
What's the point of having a throat if it creates a
retarding force?
As shown in Unified, to accelerate the flow from subsonic to supersonic, i.e., to create the high velocities associated with high thrust, one must have a converging-diverging nozzle, and hence a throat.
MP 11..16
Why isn't the stagnation temperature conserved in this
steady flow?
Heat is added in the afterburner, so the stagnation temperature increases. UnifiedTP |