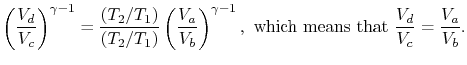|
A Carnot cycle is shown in Figure 3.4. It has
four processes. There are two adiabatic reversible legs and two
isothermal reversible legs. We can construct a Carnot cycle with
many different systems, but the concepts can be shown using a
familiar working fluid, the ideal gas. The system can be regarded as
a chamber enclosed by a piston and filled with this ideal gas.
Figure 3.4:
Carnot cycle -- thermodynamic diagram on left and schematic of the
different stages in the cycle for a system composed of an ideal gas
on the right
|
|
The four processes in the Carnot cycle are:
- The system is at temperature
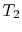 at state
at state 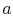 . It is
brought in contact with a heat reservoir, which is just a liquid or
solid mass of large enough extent such that its temperature does not
change appreciably when some amount of heat is transferred to the
system. In other words, the heat reservoir is a constant temperature
source (or receiver) of heat. The system then undergoes an
isothermal expansion from
. It is
brought in contact with a heat reservoir, which is just a liquid or
solid mass of large enough extent such that its temperature does not
change appreciably when some amount of heat is transferred to the
system. In other words, the heat reservoir is a constant temperature
source (or receiver) of heat. The system then undergoes an
isothermal expansion from 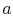 to
to 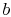 , with heat absorbed
, with heat absorbed 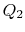 .
.
- At
state
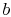 , the system is thermally insulated (removed from contact
with the heat reservoir) and then let expand to
, the system is thermally insulated (removed from contact
with the heat reservoir) and then let expand to 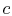 . During this
expansion the temperature decreases to
. During this
expansion the temperature decreases to 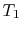 . The heat exchanged
during this part of the cycle,
. The heat exchanged
during this part of the cycle, 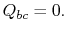 )
)
- At state
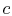 the system is
brought in contact with a heat reservoir at temperature
the system is
brought in contact with a heat reservoir at temperature 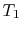 . It is
then compressed to state
. It is
then compressed to state 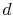 , rejecting heat
, rejecting heat 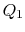 in the process.
in the process.
- Finally, the system is compressed adiabatically back to the
initial state
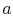 . The heat exchange
. The heat exchange 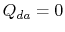 .
.
The thermal efficiency of the cycle is given by the definition
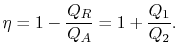 |
(3..4) |
In this equation, there is a sign convention implied. The quantities
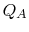 ,
, 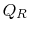 as defined are the magnitudes of the heat absorbed and
rejected. The quantities
as defined are the magnitudes of the heat absorbed and
rejected. The quantities 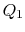 ,
, 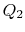 on the other hand are defined
with reference to heat received by the system. In this example, the
former is negative and the latter is positive. The heat absorbed and
rejected by the system takes place during isothermal processes and
we already know what their values are from Eq.
(3.1):
on the other hand are defined
with reference to heat received by the system. In this example, the
former is negative and the latter is positive. The heat absorbed and
rejected by the system takes place during isothermal processes and
we already know what their values are from Eq.
(3.1):
The
efficiency can now be written in terms of the volumes at the
different states as
![$\displaystyle \eta = 1+ \frac{T_1[\ln(V_d /V_c)]}{T_2[\ln(V_b /V_a)]}.$](img355.png) |
(3..5) |
The path from states 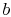 to
to 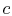 and from
and from 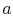 to
to 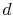 are both
adiabatic and reversible. For a reversible adiabatic process we know
that
are both
adiabatic and reversible. For a reversible adiabatic process we know
that
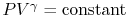 . Using the ideal gas equation of
state, we have
. Using the ideal gas equation of
state, we have
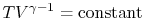 . Along curve
. Along curve
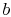 -
-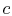 , therefore,
, therefore,
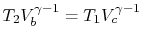 . Along
the curve
. Along
the curve 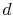 -
-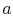 ,
,
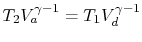 . Thus,
. Thus,
Comparing the expression for thermal efficiency
Eq. (3.4) with Eq. (3.5) shows
two consequences. First, the heats received and rejected are related
to the temperatures of the isothermal parts of the cycle by
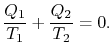 |
(3..6) |
Second, the efficiency of a Carnot cycle is given compactly by
 |
(3..7) |
The efficiency can be 100% only if the temperature at which the
heat is rejected is zero. The heat and work transfers to and from
the system are shown schematically in
Figure 3.5.
Figure 3.5:
Work and heat transfers in
a Carnot cycle between two heat reservoirs
|
|
Muddy Points
Since
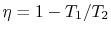 , looking at the
, looking at the  -
-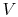 graph, does
that mean the farther apart the
graph, does
that mean the farther apart the 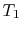 ,
, 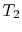 isotherms are, the
greater efficiency? And that if they were very close, it would be
very inefficient? (MP 3.2)
isotherms are, the
greater efficiency? And that if they were very close, it would be
very inefficient? (MP 3.2)
In the Carnot cycle, why are we only dealing with volume changes and
not pressure changes on the adiabats and isotherms?
(MP 3.3)
Is there a physical application for the Carnot cycle? Can we design
a Carnot engine for a propulsion device?
(MP 3.4)
How do we know which cycles to use as models for real processes?
(MP 3.5)
Douglas Quattrochi
2006-08-06
|