16.2 Introduction to Conduction
We will start by examining conduction heat transfer. We must first
determine how to relate the heat transfer to other properties
(either mechanical, thermal, or geometrical). The answer to this is
rooted in experiment, but it can be motivated by considering heat
flow along a ``bar'' between two heat reservoirs at 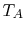 ,
, 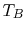 as
shown in Figure 16.2. It is plausible that the
heat transfer rate,
as
shown in Figure 16.2. It is plausible that the
heat transfer rate, 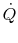 , is a function of the temperature of
the two reservoirs, the bar geometry and the bar properties. (Are
there other factors that should be considered? If so, what?). This
can be expressed as
, is a function of the temperature of
the two reservoirs, the bar geometry and the bar properties. (Are
there other factors that should be considered? If so, what?). This
can be expressed as
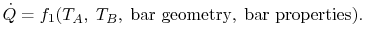 |
(16..1) |
It also seems reasonable to postulate that 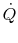 should depend
on the temperature difference
should depend
on the temperature difference 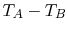 . If
. If 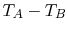 is zero,
then the heat transfer should also be zero. The temperature
dependence can therefore be expressed as
is zero,
then the heat transfer should also be zero. The temperature
dependence can therefore be expressed as
![$\displaystyle \dot{Q} = f_2[(T_A - T_B),\;T_A,\;\textrm{bar geometry},\;\textrm{bar properties}].$](img1831.png) |
(16..2) |
Figure 16.2:
Heat transfer along a bar
|
|
An argument for the general form of 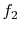 can be made from physical
considerations. One requirement, as said, is
can be made from physical
considerations. One requirement, as said, is 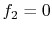 if
if 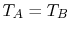 . Using a MacLaurin series expansion, as follows,
. Using a MacLaurin series expansion, as follows,
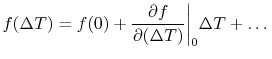 |
(16..3) |
If we define
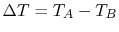 and
and 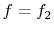 , we find that (for
small
, we find that (for
small 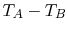 ),
),
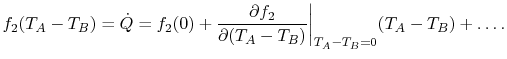 |
(16..4) |
We know that
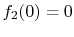 . The derivative evaluated at
. The derivative evaluated at 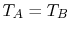 (thermal equilibrium) is a measurable property of the bar. In
addition, we know that
(thermal equilibrium) is a measurable property of the bar. In
addition, we know that
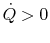 if
if 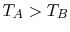 or
or
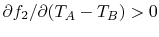 . It also seems reasonable that if we had
two bars of the same area, we would have twice the heat transfer, so
that we can postulate that
. It also seems reasonable that if we had
two bars of the same area, we would have twice the heat transfer, so
that we can postulate that 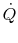 is proportional to the area.
Finally, although the argument is by no means rigorous, experience
leads us to believe that as
is proportional to the area.
Finally, although the argument is by no means rigorous, experience
leads us to believe that as 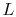 increases
increases 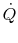 should get
smaller. All of these lead to the generalization (made by Fourier in
1807) that, for the bar, the derivative in
Equation (16.4) has the form
should get
smaller. All of these lead to the generalization (made by Fourier in
1807) that, for the bar, the derivative in
Equation (16.4) has the form
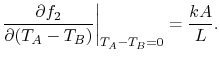 |
(16..5) |
In Equation (16.5), 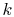 is a proportionality
factor that is a function of the material and the temperature,
is a proportionality
factor that is a function of the material and the temperature, 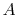 is the cross-sectional area and
is the cross-sectional area and 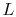 is the length of the bar. In the
limit for any temperature difference
is the length of the bar. In the
limit for any temperature difference 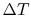 across a length
across a length
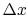 as both
as both 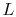 ,
,
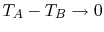 , we can say
, we can say
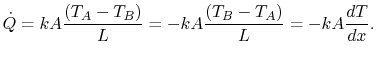 |
(16..6) |
A more useful quantity to work with is the heat transfer per unit
area, defined as
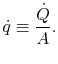 |
(16..7) |
The quantity 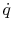 is called the heat flux and its units
are Watts/m2. The expression in
(16.6) can be written in terms of heat flux as
is called the heat flux and its units
are Watts/m2. The expression in
(16.6) can be written in terms of heat flux as
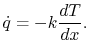 |
(16..8) |
Equation (16.8) is the one-dimensional form of
Fourier's law of heat conduction. The proportionality
constant 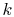 is called the thermal conductivity. Its units are
is called the thermal conductivity. Its units are
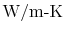 . Thermal conductivity is a well-tabulated property
for a large number of materials. Some values for familiar materials
are given in Table 16.1; others can be
found in the references. The thermal conductivity is a function of
temperature and the values shown in
Table 16.1 are for room temperature.
. Thermal conductivity is a well-tabulated property
for a large number of materials. Some values for familiar materials
are given in Table 16.1; others can be
found in the references. The thermal conductivity is a function of
temperature and the values shown in
Table 16.1 are for room temperature.
Table 16.1:
Thermal conductivity at room temperature
for some metals and non-metals
| Metals |
Ag |
Cu |
Al |
Fe |
Steel |
|
|
| |
420 |
390 |
200 |
70 |
50 |
|
|
| Non-metals |
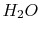
|
Air |
Engine oil |
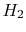
|
Brick |
Wood |
Cork |
| |
0.6 |
0.026 |
0.15 |
0.18 |
0.4-0.5 |
0.2 |
0.04 |
|
UnifiedTP
|

