Moving phosphors on the screen –
now I understand
“It has a dynamic plot – literally!”
Convolution Haiku:
Lines blue, red, and green
Moving phosphors on the screen –
now I understand
On this page, we show the convolution of a radar chirp with a chirp detector. The signals are shown in this plot; the convolution operation is shown in this movie. You can read an explanation of what's happening here.
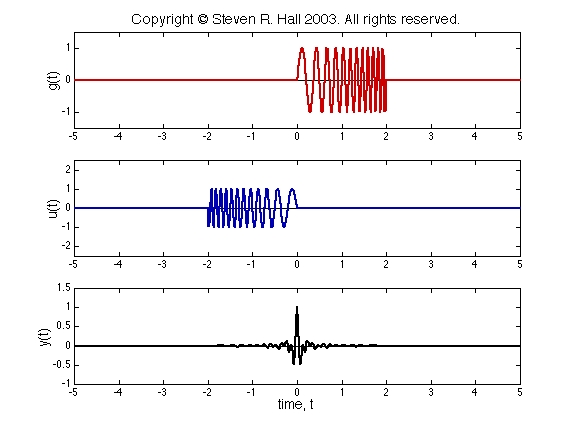
In the movie above, there are three dynamic plots. In the upper plot, u(t) is shown in blue, and g(t-τ) is shown in red. As t increases, the curve g(t-τ) slides to the right. In the middle plot, the product g(t-τ)u(τ) is shown in green. So the convolution y(t)=g(t)*u(t) at time t is equal to the area under the green. As t increases, the convolution is plotted out in the bottom plot as the black curve.
The impulse response g(t) is known as a chirp, or swept sine. It's called a chirp, because if it's an sudio signal, it makes a chirping sound. (Well, perhaps it's a little more like a whoop.) The input u(t) is the pulse sent out by the radar. It's intentially chosen to be a time reversed version of g(t). That guarantees that the maximum of y(t) is at t=0. Also, because the chirp has a broad frequency content, y(t) is large only near t=0. That makes it easy to tell when the pulse occurs.