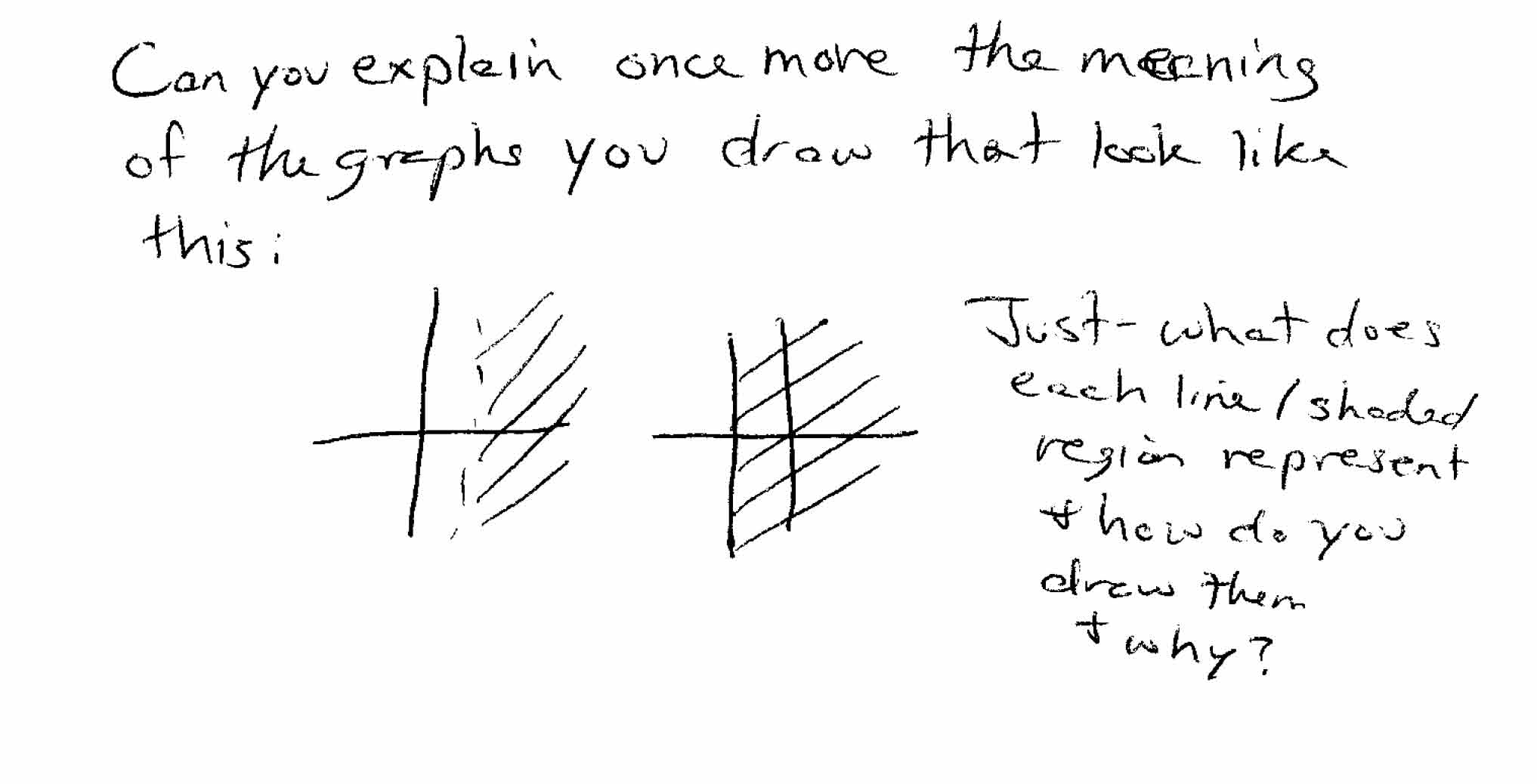Today, we talked about the relationship between BIBO stability and the
region of convergence. The neat result is that a system is BIBO
stable if and only if the region of convergence of the Laplace
transform of the impulse response contains the line
Re[s] = 0.
(17 cards) 
-
What is the region of convergence? (1 student)
It's the set of all values of
s for which the Laplace
transform integral converges.
-
Why does it matter that the LT integral converges
absolutely as opposed to just converges? (1)
Even though the LT might converge (but not absolutely) at the
boundaries of the region of convergence, in the interior it will
generally converge absolutely, because the integrand will be
exponentially smaller (as
t goes to either
+
 or
-
or
-  ) than at
the boundary of the r.o.c. That's good, because if the interior of the
r.o.c. includes
Re[s] = 0, then absolute convergence of the LT
is the same as convergence of
) than at
the boundary of the r.o.c. That's good, because if the interior of the
r.o.c. includes
Re[s] = 0, then absolute convergence of the LT
is the same as convergence of
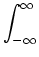 | g(t)| dt | g(t)| dt |
|
-
Stop proving everything. We believe you. (1)
But you need to understand why these things works. It's not
satisfactory for me to just claim something is true -- you shouldn't
believe it unless I prove it.
-
So a system is stable if and only if the input and
output is BIBO. But you know input / output is BIBO if and only if
area of impulse response is finite, which means the region of
convergence of
G(s) includes
Re[s] = 0. Is this correct? (1)
Very close. A system is BIBO stable if and only if the area
of the absolute value of the impulse response of the impulse response,
which is true if and only if the region of convergence of
G(s) (the
LT of
g(t)) includes
Re[s] = 0.
-
Why do we define BIBO [stability] to be what it is? (1)
Two reasons: (1) The definition is reasonable, and (2) the
definition leads to a mathematically tractable result. Not every
reasonable definition is mathematically tractable!
-
So we can now determine if a system is stable. What is
the real world application? (1)
Every control system in the real world must be designed to
make the resulting closed-loop system stable.
-
If the impulse response must converge absolutely for
the system to be BIBO stable, are systems with impulse response that
are convergent (but not absolutely) conditionally stable, or
partially stable? What does it mean to be partially stable? (1)
First, I think you mean the integral of the impulse response
converges absolutely, not that the impulse response converges
absolutely. Second, there are definitions that lead to the idea of
neutral stability, which you called partial stability. Neutral
stability is a tricky idea, though. For example, a system with a
single pole at
s = 0 is neutrally stable, but one with two poles ate
s = 0 is not. It's easier to work with BIBO stability.
-
Can you explain once more the meaning of the graphs you
draw that look like this:
(1)
The axes represent the complex plane, of the variable
s.
The vertical axis represents
Re[s] = 0; the horizontal axis
represents
Im[s] = 0. The hashed region represents the region
of convergence (of the Laplace transform of some signal,
g(t)).
Since
G is stable if and only if the LT of
g(t) has r.o.c. that
includes
Re[s] = 0, the plot on the right indicates a stable
system.
-
What is a pole? What is the
j
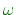 axis? (1)
A pole is (roughly) where a function
G(s) is infinite. So
the function
1/s has a pole at
s = 0. As to the second question,
any complex number
s can be represented as
s =
axis? (1)
A pole is (roughly) where a function
G(s) is infinite. So
the function
1/s has a pole at
s = 0. As to the second question,
any complex number
s can be represented as
s =  + j
+ j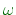 ,
where
,
where
 is the real part of
s, and
is the real part of
s, and
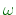 is the imaginary
part. The
j
is the imaginary
part. The
j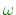 axis is the axis where
axis is the axis where
 = 0 -- it's the
vertical axis.
= 0 -- it's the
vertical axis.
-
Still confused about why the system is stable if its
region of convergence includes
Re[s] = 0. (1)
The answer is probably too long for a mud response. Briefly,
a system is BIBO stable if and only the integral
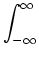 | g(t)| dt | g(t)| dt |
|
is finite. The integral is finite if and only if the integral
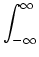 g(t)e-st dt g(t)e-st dt |
|
converges absolutely for
Re[s] = 0, since
| e-st| = 1 for
Re[s] = 0.
-
If
u(t) = 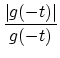 |
|
isn't
u(t) undefined for
g(- t) = 0? (1)
Yes. If I had been a little more careful, I would have
defined
u(t) = 0 for that case. The proof is still basically correct.
-
Why does
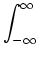 | g(t)e-j | g(t)e-j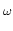 t| dt = t| dt =  | g(t)| dt | g(t)| dt |
|
(1)
Because
| e-j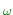 t| = 1.
t| = 1.
-
Why did you write the integrals today as
instead of
(1)
Because I was dealing with causal systems. It doesn't really
change anything.
-
No mud. (4)
A few comments:
Please don't lower your voice when
answering a question.
OK, will do.
I think board
work is good, but 1/2 the time should be used for Q & A.
I
can't promise it will be 50/50, but you make a good point, and we'll
do some of each.
When working at the board in recitation, I
would rather have a few minutes explanation (just of the setup) of the
problem to make sure that I understand what my group has done and that
it's correct.
We can try to do that, too.
Steven R. Hall
2004-05-16