18.06 Problem Set 6

Problem 1 (5+5+5+5+5 points)

In this problem, you will use least-square fitting to examine the original 1662 data demonstrating Boyle's law: the volume $v$ of a gas is inversely proportional to the pressure $p$ (for constant mass and temperature).

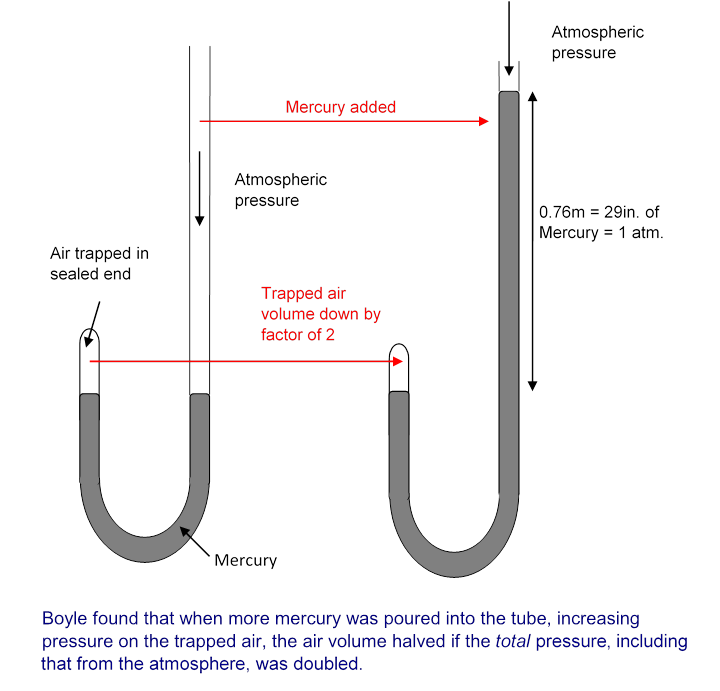
In that experiment, described here (UVa), Robert Boyle measured the volume of air trapped in the sealed end of a glass tube as they poured mercury in the other end. The total pressure $p$ on the trapped air is proportional to the height of the mercury, plus the height of mercury balancing atmospheric pressure (as measured by a Torricelli barometer). They found that the volume of the gas varied inversely with $v$. The experiment is depicted here:

(a) Open Boyle's 1662 manuscript, find the chapter on the "new experiment", and locate the experimental data, which is labelled A Table of the Condensation of Air. Extract the data from the first column "A" and enter it into a Julia array v below — this is the height of the air column, proportional to its volume. (There is a second column "A" that contains the same data divided by 4.) Extract the data from the column "D" and enter it into a Julia array p below — this is the height of the mercury column (including the amount corresponding to atmospheric pressure), and is proportional to the total pressure.

(b) Perform a least square fit to the model $v = \alpha / p$, i.e. find α that minimizes the sum of the squared error $\sum_k (v_k - \alpha/p_k)^2$ for Boyle's data points $(p_k, v_k)$. (Note: in Julia, you can make a vector of the inverse pressures with 1 ./ p.) Plot the data and the fit ($v$ vs. $p$) using the provided code below.

Note: if you find yourself using calculus here or in subsequent parts, you are re-inventing the wheel — we already derived how to minimize the squared error in class, so please re-write it as a matrix least-squares problem and use the 18.06 results.

(c) Perform a least-square fit to a more complicated model, $v = \frac{\alpha}{p} + v_0$, for fit parameters α and v₀. (That is, suppose that Boyle was slightly wrong, and that there is a minimum volume v₀ even for $p \to \infty$, similar to van der Waals equation.) What α and v₀ do you obtain?

(d) If the gas in Boyle's experiment exactly obeyed Boyle's law, i.e. if the theoretically correct $v_0$ is 0 in part (c), would you expect to get $v_0 = 0$ from a least-square fit of experimental data? Why or why not? (No detailed math please, just a sentence or two of explanation.)

(e) Alternatively, suppose we don't know the power law in our model: suppose $v = \alpha p^n$ for an unknown power $n$ and an unknown coefficient $\alpha$. This depends nonlinearly on $n$, so at first glance it may seem that we cannot do a linear least-square fit using 18.06 techniques. However, show that $\log v$ depends linearly on two unknown fit parameters in this model, and hence do a least-square fit of $\log v_k$ to the log of the model to estimate the parameters $\alpha$ and $n$ from Boyle's data. Note: in Julia, you can take the log of every element of an array v with log.(v).

# part (a):

v = [ ... ] # data from Boyle table, column A
p = [ ... ] # data from Boyle table, column D

# part (b)

α = ... # least-square fit

# part (b) plot

using Plots   # you might have to install it first: import Pkg; Pkg.add("Plots")

plot(p, v, seriestype = :scatter, label="data", title = "Problem 1(b): Boyle's Law fit", fmt=:png)
plot!(p, α ./ p, label="fit $(round(α,sigdigits=3))/p")
xlabel!("pressure (mercury height, in)")
ylabel!("gas volume (height, in)")

Problem 2 (5+5 points)

Let $q$ be some unit vector (i.e. $\Vert q \Vert = 1$). Define the "reflector" matrix: $$ F = I - 2qq^T $$

(a) Show that $F$ is unitary.

(b) Why is this a "reflector"? Suppose that we are in 2 dimensions (i.e. $q \in \mathbb{R}^2$). Draw a picture showing $q$ pointing in some arbitrary direction, and sketch $x$ and $Fx$ for three cases: when $x$ is parallel to $q$, perpendicular to $q$ (and nonzero), or in some other direction (neither parallel nor perpendicular to $q$).

Problem 3 (6+4 points)

From Strang, section 4.3, problem 27 (distance between lines):

The points $p(\alpha) = \begin{pmatrix} \alpha \\ \alpha \\ \alpha \end{pmatrix}$ and $q(\beta) = \begin{pmatrix}\beta \\ 3\beta \\ -1 \end{pmatrix}$, as a function of the scalars $\alpha,\beta$, form two lines in space that never meet.

(a) Choose $\alpha$ and $\beta$ to minimize the squared distance $\Vert p - q\Vert^2$.

• Express this problem in matrix form as minimizing $$\Vert Ax - b\Vert^2$$ for some vector $x$, some matrix $A$, and some vector $b$.
• Solve the normal equations $A^T A \hat{x} = A^T b$ to find the minimizer $\hat{x}$.

(b) The line connecting the closest points $p(\hat{\alpha})$ and $q(\hat{\beta})$ is perpendicular to ________________.

Problem 4 (6+4 points)

(From Strang, section 4.4, problem 18.)

(a) Find orthonormal vectors $q_1, q_2, q_3$ by Gram-Schmidt from $a_1, a_2, a_3$ given by: $$ a_1 = \begin{pmatrix} 1 \\ -1 \\ 0 \\ 0 \end{pmatrix}, \; a_2 = \begin{pmatrix} 0 \\ 1 \\ -1 \\ 0 \end{pmatrix}, \; a_3 = \begin{pmatrix} 0 \\ 0 \\ 1 \\ -1 \end{pmatrix}, $$ which are a basis for the vectors perpendicular to $d = \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \end{pmatrix}$, i.e. a basis for the nullspace of ______________.

(b) If you form the $4\times 3$ matrix $Q = \begin{pmatrix} q_1 & q_2 & q_3 \end{pmatrix}$, then what is $Q^T d$? (No arithmetic is required — think about it!)