Assignment 2: Grid of Resistors



Life is too short to spend writing do loops.
-- Cleve Moler, 1993


The main goal of this assignment is to convince you of the ease of use of the data parallel programming model. For those problems that lend themselves to this model, programming a parallel machine can be easier than programming serial machines. Copy all of the files in my directory on scout for Homework #2 by executing the command (in your own appropriate directory).

cp ~edelman/1995/HW2/*.fcm

You should obtain four cmf files. Each one of these files is performing the same operation. It is computing the effective resistance and voltages of a grid of resistors. Each program is only one page long. Also please note the assignment checklist at the end of this document. We will also use some timing routines. To understand what these routines are measuring as well as the syntax of the commands see pages 33-35 of the CM-5 CMF Performance Guide. You will notice some write statements that are commented out towards the end of the program. You may choose to remove the comments to "see" the resistance.

The problem is to compute the voltages and the effective resistance of a 2n+1 by 2n+2 grid of 1 ohm resistors if a battery is connected to the two center points. This is a discrete version of finding the lines of force using iron filings for a magnet.


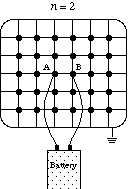
A contour plot of the answer (for a larger value of n) looks like


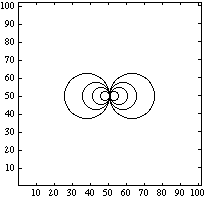
The method of solution that we will use here is successive overrelaxation (SOR) with red-black ordering. This is certainly not the fastest way to solve the problem, but it does illustrate many important programming ideas.

It is not so important that you know the details of SOR. (Some of the basic ideas may be found on pages 407-409 of Gil Strang's Introduction to Applied Mathematics, somewhat more in depth discussion may be found any serious numerical analysis text such as Stoer and Bulirsch's Introduction to Numerical Analysis.) What is important is that you see that the nodes are divided in half into red nodes and black nodes. During the first pass, the red nodes obtain the voltages as a weighted average of their original voltage, the input (if any) and the four surrounding black nodes. During the second pass, the black nodes obtain voltages from the four surrounding red nodes. In the infinite limit, the process converges to the correct answer.

Let us have a look at the first two programs sor_cshift and sor_eoshift. These programs define a 2n+1 by 2n+2 matrix v for voltages, and two logical arrays, red and black for the red/black nodes. The first and last rows and columns (the boundary) are never modified, they are "grounded", have voltage 0. The difference in the two programs is only that while in the first one the voltage of the neighbors is added by cshift, the second uses eoshift for the same thing. Last year, we assigned this problem to 18.337 and found a big difference in the performance in the two codes. It is a nuisance that such small choices can radically affect the performance. If you try it now you will probably see that the cshift version is only slightly faster than the eoshift version.

The third program sor_arraysection uses a quite different approach: both reds and blacks are determined as two array section ("odds and evens"). Information from neighbors is obtained directly through shifting the array sections.

We would like you to time say 200 (or whatever you like) iterations by the CM_timers. The time for array sections is very bad; array sections as they are implemented on the CM-5 incur a huge amount of overhead.

Your first programing assignment is the following: implement the analogous problem on a 2n+1 by 2n+1 by 2n+2 grid in three dimensions. Pick whichever code or code you prefer. This may still be done with two colors. The value of the optimal mu you have to use is 2*cos(pi/(2*n))+cos(pi/(2*n+1)))/3. Next solve the problem in four dimensions, with mu = (3*cos(pi/(2*n))+cos(pi/(2*n+1)))/4. Can you guess the effective resistances of the various meshes as n --> infinity ?

Now this gets harder. In our cshift and eoshift programs we use the where(reds) statement. Though you might have imagined that the compiler is smart enough to work in time proportional to the active part (i.e. the "true" part) of the statement, unfortunately it is not. In fact, the time spent is proportional to the entire size and even more time for conditioning.

We would like you to improve the program by putting all the red nodes into one array called red and all the black nodes in the same size array black. The data arrangement is given in Figure 1 for the general case, and in Figure 2 for n=4. For simplicity we require n to be even.


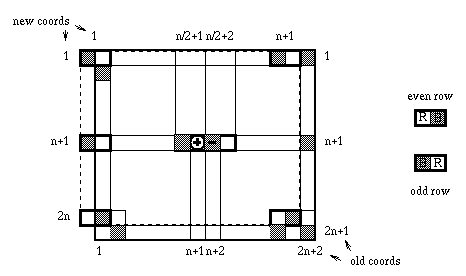
Figure 1. The data arrangement with 2 arrays



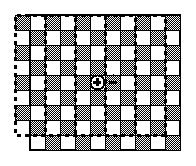
nFigure 2. The case of Figure 1, for n = 4


This arrangement is in our program sor_2arrays. Unfortunately, timing is not improved; use the timers to discover which is the really slow part of the program. Try to see if you can improve the program, using two arrays and CSHIFT only. Or try using four arrays, two for the even rows of red and black, two for the odd rows.

Assignment Checklist