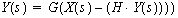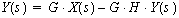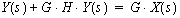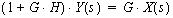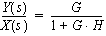Block Diagram Fundamentals

2.010 Modeling Dynamics and Control III
SPRING 2001
Block Diagram Fundamentals

Going through the (simple!) algebra to derives Black's formula for closing a negative feedback loop is a very worthwhile exercise. 'Block diagram algebra' ain't called 'algebra' for nothing: it's just a graphical way of representing algebraic equations.

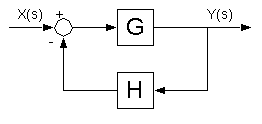
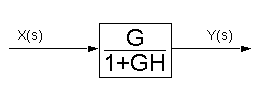
At left below is a generic negative feedback system.	'Closing the loop' results in the simplied system at the right.

First, we will write a (standard) algebraic equation representing the system at left;

In other words, the output, Y(s), is 'G' times the quantity X(s) minus 'H' times that same output Y(s).

Now we place all terms in Y(s) on one side of the equation; X(s) on the other.

Therefore, the transfer function from X(s) to Y(s):is:

This is an incredibly useful shortcut for the simplification of feedback systems. If you feel comfortable with block diagram algebra, you should have no problem rederiving this formula from scratch (although it's quite likely you'll just end up memorizing it - it's used so frequently in controls).

Last updated February 19, 2001.