A flat plate is hinged at one side to s smooth floor, as shown, and held at a small angle q_o (q_o<< 1) relative to the floor. The entire system is submerged in a liquid of constant density r.  At t = 0, a vertical force is applied and adjusted continually so that the rate of decrease of the plate angle q remains constant at a value :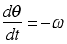

Assuming that the flow is incompressible and inviscid, derive expressions for

(a) the horizontal velocity u(x,t) at point x and time t

(b) the x-direction force F_H(t) exerted by the hinge on the floor. Assume the plate has negligible inertia.