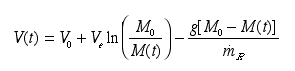|
 |
After its second booster has been fired, a space
vehicle finds itself outside the earth's atmosphere moving vertically
upward against gravity 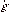 at speed
V0. Its total mass at that point is M0. At
t = 0, the vehicle's third stage is turned on and the rocket burns propellant
at a mass rate of at speed
V0. Its total mass at that point is M0. At
t = 0, the vehicle's third stage is turned on and the rocket burns propellant
at a mass rate of 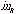 kg/s.
Show that if the gravitational acceleration remains essentially constant
at the rocket during the firing, the rocket’s velocity V(t)
after time t will be given by kg/s.
Show that if the gravitational acceleration remains essentially constant
at the rocket during the firing, the rocket’s velocity V(t)
after time t will be given by
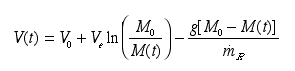
where M(t) is the mass of the system at
time t. Note that the pressure of the gas at the rocket exit plane,
pe, will not be zero as it is in the ambient
space, since the rocket exhaust is supersonic and hence the pressure at
the exit is not in balance with the ambient pressure. The answer given
above neglects the effect of the exit plane pressure on thrust.
|
 |
 |