 |
 |
A combustible mixture of air and fuel is initially
at rest at a density r1 and uniform pressure
p∞. At t = 0, the mixture is ignited at
the origin by a spark and a flame front begins to move radially outward
from the origin at a constant speed Vf. As the
flame front overtakes a gas particle, it converts the combustible mixture
of density r1
to a hotter combustion product of lower density r2.
This occurs so fast that the flame front can be modeled as an infinitesimally
thin density discontinuity. Because the volume of a fluid particle increases
as it is enveloped by the flame front, the combustible mixture ahead of
the expanding flame front is pushed radially outward by the front. The
combustion products of density r2 that
are left behind the flame must, however, be stationary relative to the
reference frame fixed in the origin.
(a) In a reference frame fixed in the origin,
determine the radial outflow velocity v(r,t) of the combustible
mixture. There will be different expressions for the unburned gas ahead
of the flame front (r > Vft) and the burned gas
left behind (r < Vft). See also Prob. 3.17. Show
that the velocity distribution can be expressed in the dimensionless form
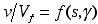 , where , where
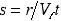 is
either a dimensionless radial distance at fixed time or a dimensionless
inverse time at fixed r, and is
either a dimensionless radial distance at fixed time or a dimensionless
inverse time at fixed r, and 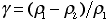 is
a dimensionless density difference between the unburned and burned gases. is
a dimensionless density difference between the unburned and burned gases.
|
 |
 |