 |
 |
| SUCKER ROD PUMP | ||
| QUESTIONS OR COMMENTS | ||
 |
AUTHOR: | Sergio A. Diaz |
| E-MAIL: | sadiaz@MIT.EDU | |
| COURSE: | 2 | |
| CLASS/YEAR: | 3 | |
MAIN FUNCTIONAL REQUIREMENT: Draw subterranean fluid to surface.
DESIGN PARAMETER: Sucker Rod Pump
Pump consisting of four bar linkage, plunger, and valve assemblies.
GEOMETRY/STRUCTURE:
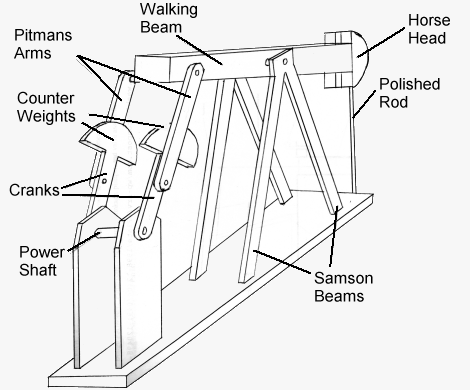 |
| Figure A Components of Sucker Rod PumpA motor and gearbox supply power to turn the power shaft. There is a counterweight at the end of the crank. A pitman arm is attached to the crank and it moves upward when the crank moves counterclockwise. The Samson arms support the walking beam. The walking beam pivots and lowers or raises the plunger. The rod attaches the plunger to the horsehead. The horsehead (not rigidly attached) allows the joint (where rod is attached) to move in a vertical path instead of following an arc. Every time the plunger rises, oil is pumped out through a spout. The pump consits of a four bar linkage is comprised of the crank, the pitman arm, the walking beam, and the ground. |
EXPLANATION OF HOW IT WORKS/ IS USED:
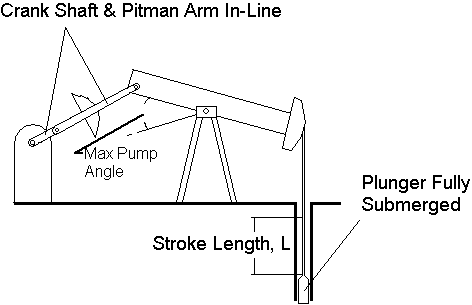 |
| Figure B: Operational Detail of Sucker Rod Pump Here the plunger is shown at its lowest position. The pitman arm and the crank are in-line. The maximum pumping angle, denoted as theta in the calculations, is shown. L is the stroke length. After one stroke, the plunger moves upward by one stroke length and the walking beam pivots. The crank also rotates counterclockwise. At the end of the upstroke the pitman arm, the crank, and the walking beam are in-line. |
For name and location of parts, see Figure A.
- A motor supplies power to a gear box. A gearbox reduces the angular velocity and increases the torque relative to this input.
- As shown in Figure B, (the crank turns counterclockwise) and lifts the counterweight. Since the crank is connected to the walking beam via the pitman arm, the beam pivots and submerges the plunger. Figure B also shows the horsehead at its lowest position. This marks the end of the down stroke. Note that the crank and the pitman arm are in-line at this position.
- The upstroke raises the horsehead and the plunger, along with the fluid being pumped. The upstroke begins at the point shown in Figure B. At the end of the upstroke, all joints are in-line. This geometric constraint determines the length of the pitman arn.
- Figures C(a) and C(b) show the plunger and ball valves in more detail. These valves are opened by fluid flow alone. On the upstroke, the riding valve is closed and the standing valve is open. Fluid above and within the plunger is lifted out of the casing while more fluid is pumped into the well. On the down stroke, the riding valve is opened and the standing valve is closed. Fluid flows into the plunger and no fluid is allowed to leave the well.
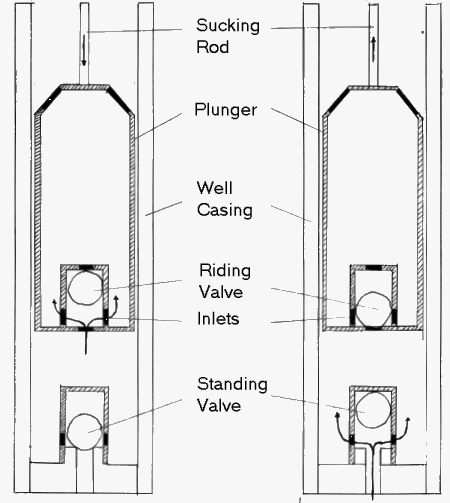 |
|
| Figure C(a) | Figure C(b) |
DOMINANT PHYSICS & DESIGN:
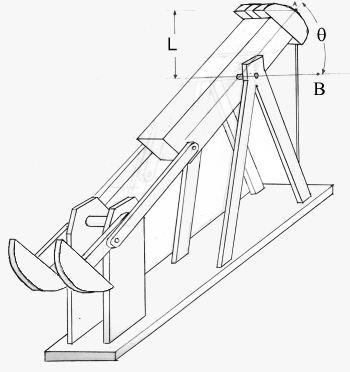 |
| Figure D: Variable Descriptons For SRP |
Table 1: Variable Descriptions, Values and Units
| Variable | Description | Typical Value | Units |
| q | Full Pump Angle | --- | degrees |
| Fl | Total Force Pump must exert | --- | lbs |
| Ff | Weight of Fluid | --- | lbs |
| Fr | Weight of the Rods | --- | lbs |
| Fc | Weight of counterweight | --- | lbs |
| Fb | Buoyant force on rods | --- | lbs |
| w | Rod weight per unit length | --- | lbs/ft |
| Lr | Length of one rod | 25 - 30§ | ft |
| Nr | Number of Rods | --- | --- |
| Pi | Input Power | 4000§§ | psi |
| h | Depth of Well | 10,000§§§ | ft |
| r | Fluid Density | --- | lbm/in^3 |
| g | Gravitational Acceleration Constant | ~9.8 | m/s^2 |
| L | Stroke Length | 16 - 192§§§§ | in |
| T | Required Pumping Torque | 6,400 - 912,000§§§§§ | in-lb |
| Vf | Fluid Volume per Stroke | --- | ft^3 |
| Ar | Rod Cross sectional area | --- | psi |
| Sy | Yield Strength of Rod | --- | psi |
| Ap | Plunger Cross Sectional Area | --- | psi |
§ Reference 1, pp. 9.279
§§ Reference 1, pp. 9.277
§§§ Reference 1, pp. 9.277
§§§§ Reference 1, pp. 9.282
§§§§§ Reference 1, pp. 9.282
To design a sucker rod pump, the depth of the well must first be determined. This value is then used to calculate the amount of fluid that can be pumped per stroke. This amount is the volume of fluid that fits in a cylinder of height L and cross sectional area Ap.
Vf = Ap L
This volume is then multiplied by the density of the fluid and by the g to find the weight of the column of fluid the pump must lift.
Ff = Mf r g
The pump must also provide enough power to lift the sucker rods (see Figure A). Manufacturers specify typical values of weight per unit length, w, for the rods they make. This number is multiplied by the length of one rod, Lr, and by the number of rods, Nr.
Fr = w Lr Nr
Since the rods are submerged in fluid, a buoyant force is present. This force is found using Archimedes’ Principle. It states that the buoyant force a submerged object feels is equal to the weight of the fluid it displaces. Therefore, the volume of displaced fluid is equal to the submerged volume of the rods. The weight of this fluid is equal to this volume multiplied by the fluid’s density and g. To obtain the volume of the rods, we multiply their cross sectional area by their total length.
Fb = Ar Nr Lr r g
Now the total load the pump must lift can be calculated.
Fl = Ff + (Fr – Fb)
Two things must be noted. First, the above analysis is very rough and does not include additional factors such as impulse forces. For more detail, see Reference 1, page 9.283. Also, the forces described above vary with time and this must be taken into account.
The stroke length of the pump is the vertical distance the plunger travels in one stroke. This length depends on the amount of fluid being pumped. Once the stroke length is known, the geometry of the four bar linkage can be determined. To avoid excessive wear of the machinery, it is good engineering practice to reduce the number of cycles the pump completes per unit of time. In order to do this more fluid should be pumped per cycle. In order to increase the fluid displacement, the stroke length should be maximized. Typical values for stroke length vary from 16 to 192 inches (see Reference 1, pp. 9.282). The stroke length can be used to calculate the torque required to pump the oil according to the following formula.
T = C L Fl
Here, C is a function of the geometry of the four bar linkage and the force the counterweight exerts on the crank (see Reference 1, pp. 9.283). Typical values for torque range from 6,400 to 912,000 in-lb (see Reference 1, pp. 9.282).
On the upstroke, two forces help pump the oil from the well. The first is the "force" supplied from the torque produced by the motor and gearbox. The second force comes from the weight of the counterweight as it falls (see Figure C).
LIMITING PHYSICS:
Care must be taken to choose a cross sectional area large enough so that the rods do not yield. This area can be found by dividing the total tensile load by the yield stress of the material.
Ay = Fl / Sy
The area of the rods must be greater than this area. This is a minimum. Fatigue affects (function of material and loadking) will require a larger value.
EFFICIENCY:
The efficiency of the sucker rod pump can be defined as the volume of oil it actually pumps divided by the volume it can theoretically pump. When the well is initially drilled, the oil contains a lot of gas. This gas displaces a small volume of oil at the beginning. This volume decreases eventually. The volumetric efficiency of this type of pump is rated at about 80%. (see Reference 1, pp. 9.277)
PLOTS/GRAPHS/TABLES:
None Submitted
WHERE TO FIND SUCKER ROD PUMPS:
Sucker rod pumps are used primarily to draw oil from underground reservoirs. The mechanisms it employs however are found in a wide variety of machines. The four bar linkage can be found on door dampers, on automobile engines, and on devices such as the lazy tong. The Sterling engines manufactured in 2.670 also use a linkage similar to the one used by the pump.
REFERENCES/MORE INFORMATION:
1) Karassik, Igor J. et al, Pump Handbook. pp. 9.278-9.285, McGraw-Hill, New York, 1986.
2) Sucker Rod Pump (From the Internet Glossary of Pumps)
URL: http://www.animatedsoftware.com/pumpglos/suckerro.htm