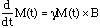Review of Free Precession - Since the individual spins are quantized along the direction of the external magnetic field (along the z-axis), then only this component of the nuclear spin has a definite value at equilibrium, the two transverse components (x and y) are in superposition states. The bulk nuclear magnetization at equilibrium is a stationary magnetic moment aligned along the z-axis.

As we have seen, the dynamics of this bulk magnetization away from equilibrium can be broken down into two simple motions,

1) a precession about the applied magnetic field associated with the torque,

,

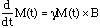and,

2) a relaxation that carries the magnetization back to equilibrium.

Since the external field is about the z-axis, the precession is around the z-axis at a frequency of,

,

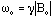the so-called Larmor frequency.

The relaxation process has two components, the magnetization along the z-axis relaxes towards its equilibrium value, M0, and the transverse components (x and y) relax towards zero. The bulk magnetization vector is composed of the magnetic moments of many individual spins and its length has a maximum which is equal to the Boltzman excess population present at equilibrium, M₀. However, the magnetization does not have a minimum value since two individual magnetic moments may be anti-parallel to one another and thereby reduce the length of the bulk magnetization vector. For instance, if the magnet homogeniety is poor, then the FID decreased quickly due to the interference of the spin magnetization from various parts of the sample, yet the z-component of the magnetization is uneffected by this. Therefore, the transverse component can relax at a faster rate than the z component does in its return to equilibrium, and two time constants are required to describe spin relaxation. These two relaxation times are called the spin-lattice relaxation time, T1, (along the z-axis) and the spin-spin relaxation time, T2, (governing the decay of transverse magnetization).

The Bloch Equations - The Bloch equations describing the complete spin dynamics are,

.

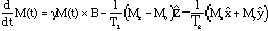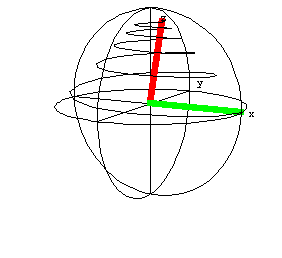
Notice that T2 must be less than or equal to T1 to conserve the maximum length of the magnetization vector. Two useful pictorial representations of the evolution of the spin magnetization back to equilibrium, after having first been placed along the x-axis are shown below.

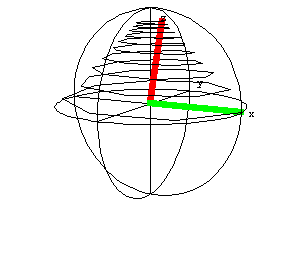
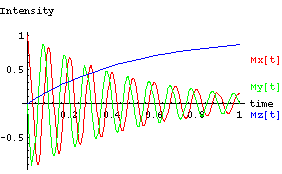
These plots are a result of a simulation run with the following parameters

T1 = 0.5 sec

T2 = 0.5 sec

wo = 20 Hz

The simulation covers times of 0 to 1 seconds.

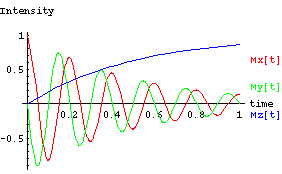
T1 = 0.5 sec

T2 = 0.5 sec

w = 10 Hz

Notice the change in the Mx and My components, but no change in the Mz-component.

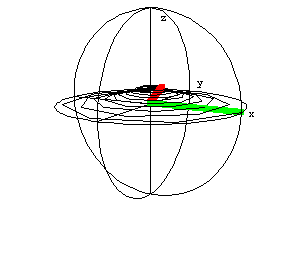
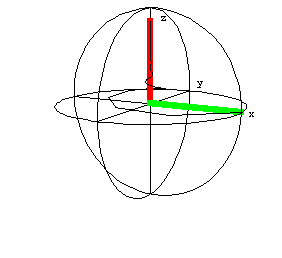
T1 = 5 sec

T2 = 0.5 sec

wo = 20 Hz

Notice only Mz(t) is changed from the first plot.

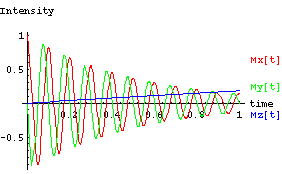
T1 = 0.5 sec

T2 = 0.05 sec

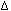wo = 20 Hz

Notice that the modulation frequency of Mx,y is the same as the first plot, but the lifetime is greatly reduced.

RF pulses - In terms of the Bloch equations notice that two types of magnetic fields have a pronounced influence on the dynamics: static fields along the z-axis, and transverse fields rotating at the Larmor frequency. Changes in the strength of the field along the z-axis result in changes in the Larmor frequency. Since the magnetization is precessing at the Larmor frequency, transverse magnetic fields that rotate about z at the same frequency (resonant fields) will create a constant torque on the spins and rotate them away from the z-axis. This second motion is most readily seen in a reference frame where the magnetization is stationary, the "rotating" frame defined by the transformation,

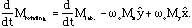
If the applied magnetic fields are separated into two components, a static field along the z-axis, B0, and a rotating field along the x-axis of the rotating frame, B1, then the Bloch equations simplify to,

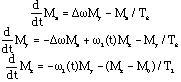
where, Dw is a small off-resonance term (the difference between the rotating frame frequency and the Larmor frequency), and w1 is the strength of the rotating field (the radio frequency field),

.

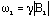The quick-time movie shows the dynamics associated with an on-resonance(w=0) RF pulse applied along the x-axis.

For simplicity, the NMR experiment is usually referenced to a frame that moves with an externally applied radio frequency field. Notice that in transforming to the rotating frame only those components that will influence the spin dynamics were kept, the fields that are static in the rotating frame. All other fields will be purely oscillatory in this reference frame, and the long time behavior of the spins will not be influenced by them.

The overall NMR experiment can be described with reference to the Block Equation. The spins are placed in a homogeneous magnetic field, and after the populations have reached equilibrium, an RF field is applied for a short time. This RF pulse rotates the bulk magnetization away from the z-axis at an angular velocity of w1. By varying the length of the RF pulse the angle can be made equal to 90°, w1 t=¹/2, (a so-called ¹/2 pulse) and the magnetization will be aligned along the y-axis. The RF field is then turned off and the spins return to equilibrium. The transverse components of the magnetization vector (Mx and My) are captured by monitoring the voltage induced in a tuned coil wrapped around the sample.

If the spins are off-resonance (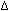w0) when a RF pulse is applied, then there is an "effective" field Beff = B1 + 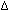B = B1 + 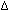w/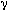. The spins naturally evolve about this effective field, not about B1.

This quick time movies show the dynamics associated with an off-resonance RF pulse applied along the x-axis.

NMR and Linearity - The measured signal, the free induction decay (FID), is in the time domain and has the form,

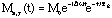. [11]

the solution to the Block Equation when B1=0.

The Fourier transformation of the FID is a Lorentzian with a width of,

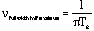. [12]

Since both the Fourier transformation and the Bloch equations in the absence of an RF field are linear, we are free to break the NMR experiment into a superposition of identical experiments on each NMR distinct set of spins. So, a general result is a frequency spectrum showing many resonances each corresponding to an identifiable spin system. The frequency differences may arise from small chemical shifts associated with the partial screening of the magnetic field by the electrons, from spin-spin couplings, or from local variations in the magnetic field strength due to the heterogeneity of the magnetic susceptibility throughout the sample. We will return to these interactions presently.

The Inversion-Recovery method of measuring T1 -

The value of T1 provides information about the molecular dynamics of the system and fundamentally limits how rapidly NMR spectra may be obtained. This constant can be measured by the sequence of ¹ - tau - ¹/2 - detect. The -pulse inverts the z magnetization which then returns to its equilibrium value during the time, tau. The final pulse is used to readout the Mz(tau) intensity. T1 is measured by making a series of measurement as a function of tau.

A quick-time movie showing the dynamics during an inversion recovery experiment.