Echoes and Multiple-Pulse Experiments

Last class we saw that selected spin dynamics could be made to run backwards in time and thus to create an echo. This was demonstrated via a "gradient" echo where after a period of time the gradient direction was inverted and the spin evolved back until they were once again in phase.

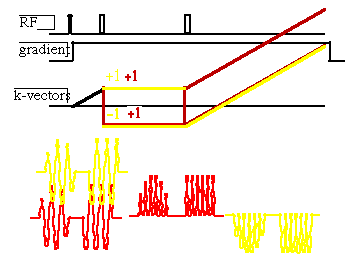
A gradient echo is generated by a bi-polar gradient waveform. Since the k-vector is the integrated area under the gradient waveform at the end of the bi-polar gradient k returns to zero, and there is no magnetization grating across the sample. At the mid-point of the gradient waveform k is maximum and the grating is at its finest. Since the NMR signal is the integration of the spin magnetization across the sample, the signal maximums correspond to the two points where k is zero, and hence an echo is observed.

Since the only interaction that is influenced by the presence of a gradient is the gradient evolution itself, the bipolar gradient waveform shown above will only refocus the gradient.

In select cases the sign of the interaction can be changed, as it was in the gradient echo, but in general refocussing is accomplished through the actions of RF pulses that strongly modulate the spin dynamics. RF pulses are normally arranged such that the RF field strength is stronger than any internal interaction and so they can be thought of as instantaneously changing the spin state of the system.

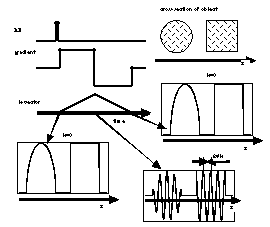
The simplest RF pulse created echo is the two pulses (¹/2,¹) sequence shown below. The first RF pulse rotates the magnetization from the z-axis into the transverse plane, where in the presence of a gradient it creates a magnetization grating. The ¹ pulse invert the sense (directionality) of this grating so that continued evolution in the magnetic field gradient leads to the formation of an echo.

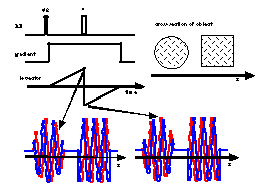
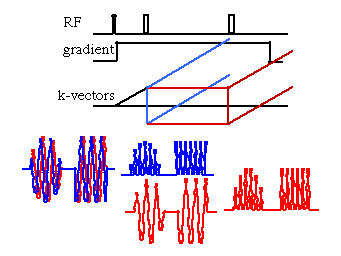
The figure shows the actions of a ¹-pulse when applied to a magnetization grating. Here both quadrature components of the transverse magnetization must be kept track of, and these are color coded blue and red in the figure. The two gratings are shown just before and just after the ¹-pulse which inverts the sign of one of the two components (the red in the figure). This is consistent with the RF pulse corresponding to a rotation of 180° about an axis in the transverse plane. Before and after the ¹-pulse and magnetization grating has the same pitch, but the sign of the grating is changed by the pulse. Following the ¹-pulse the magnetic field gradient is still in the same direction and so the k-vector continues to increase, but now towards zero, and following an equal length of time k returns to zero and all of the magnetization is again coherent. A spin echo is formed.

The spin echo will refocus any time-independent variations in the resonance frequency, including chemical shifts, susceptibility shifts, and heteronuclear spin couplings. Earlier the spin-spin relaxation time was identified with the decay of the bulk magnetization in the transverse plan, we now see that this is not a fundamental relaxation phenomena since, for example, the applications of a magnetic field gradient can increase its rate, and since the magnetization can be refocussed. The fundamental spin-spin relaxation rate is associated with those decay processes that can not be refocussed by methods such as the spin echo, and the observed decay of the transverse magnetization is the rate sum of this and other contributions,

.

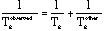One very useful imaging application of the spin echo is to change the image contrast from being a measure of the pure spin density (by using a spin echo to refocus spatial variations in the observed T2), to being dependent on the local magnetic field variations (by using a gradient echo).

The above quicktime movie shows the dynamics of 4 spin packets during a Hahn echo sequence of 90x - tau - 180x. Notice that the signal refocuses along -y.

The above quicktime movie shows the dynamics of 4 spin packets during a Hahn echo sequence of 90x - tau - 180y. Notice that the signal refocuses along +y.

Any train of RF pulse will create a pattern of echoes, that can refocus line broadening terms.

The above quicktime movie shows the dynamics of four spin packets during a 90x - tau - 90x sequence. Notice that an echo is formed from only 1/2 of the total spin magnetization.

A second application of spin echoes is to store information that can then be read out latter. The stimulated echo shown in figure 8 is a classic example of this.

Schematic view of a ¹/2, ¹/2 echo and the stimulated echo. The second ¹/2 RF pulse rotates one component of the transverse spin magnetization to the z-axis (along the field) where it does not evolve (recall that in the Bloch Eqns the z-magnetization only slowly decays). The remaining transverse magnetization is now an oscillator function of the spatial coordinate and so is a combination of +k and -k states (the blue trajectories in the figure). Likewise the z-magnetization is also a combination of +k and -k (the red lines). Between the second and third RF pulses, only the transverse components evolve, and only one half of the signal forms an echo. The third RF pulse returns the magnetization that was stored along the z-axis back into the transverse plane where it too evolves and eventually yields the "stimulated" echo. This echo has special importance, since between the second and third pulses the corresponding magnetization was stored as a spatial grating.

In addition to the stimulated echo, there are four other echoes in the stimulated echo sequence.

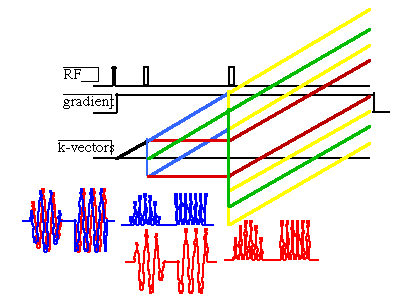
One of the most useful features of the stimulated echo is that a magnetization grating can be stored for a time comparable to the spin-lattice relaxation time (on the order of a few seconds), this is an ideal approach to measuring extremely slow processes - for instance molecular transportation over macroscopic distances.

Notice that following a 90x - tau - 90x sequence, there is a grating stored along the z-axis that may be described as a cosine modulation,

.

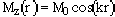If there is a coherent flow process, then during the storage time this grating is translated into,

,

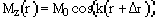which may be described as a modulation of the original grating,

.

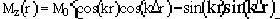So the result of a translation of the grating is an amplitude modulation of the two k-vectors that describe the modulation. this is shown in the following figure, and a translation corresponding to a 90° phase shift inverts the sign of the echo.