The NMR Microscope
There are many excellent descriptions of NMR instrumentation,
here the focus is on the changes necessary to implement microscopy
on a high resolution, high field spectrometer. Fortunately these
are quite modest, since many spectrometer have the necessary gradient
amplifiers and controllers, and all modern instruments are capable
of performing the experiments. The fundamental difference is
the NMR probe, shown schematically below.

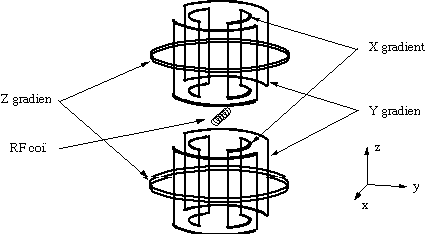
A schematic representation of the NMR microscopy probe, the magnetic
field is along the vertical axis. The probe has a small RF coil
wrapped tightly about the sample, the good filling of the coil
is necessary to reduce resistive losses in the coil. This is
surrounded by three gradient coils that are connected to audio
frequency amplifiers. The z-gradient is a Maxwell pair through
which currents flow in opposite directions. Moving inwards, the
x and y-gradient coils are each composed of four semi-circular
current paths through which currents flow in parallel.
Notice that the field of view is normally limited physically by the size of sample that can be accommodated in the RF coil. This is advantageous for sensitivity reasons, and quite necessary for reasonable experimental times. Some typical values are given in table 2.
Table 2 Some typical NMR Microscopy Probe Configurations
2-D Imaging
Having seen that by applying a magnetic field gradient one can
encode a 1-D image and collect a projection of the spin density
of the sample, one clear path to 2-D imaging is to collect a series
of such projections with the gradient at various orientations
and then to use Radon filtered back projection to reconstruct
the image. Early NMR images were acquired in this fashion, and
occasionally solid state images still are. However, most imaging
is performed via Fourier Imaging where a 2 or 3-D region of reciprocal
space is sampled corresponding to the desired resolution and field
of view. Such data are easily measured since the gradients are
under experimental control and virtually any gradient waveform
can be generated. Since the various sequences can be rather complex,
often a pictorial representation of reciprocal space is employed
where the trajectory of the experiment is mapped out. It is then
possible to focus on the manner in which 2-D k-space is sampled
rather than to get caught up in the details of the NMR experiment.
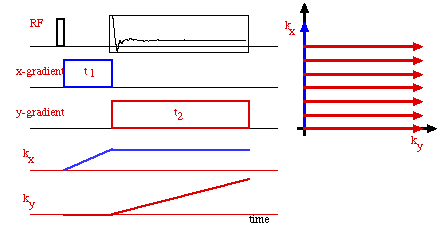
A generic 2-D Fourier imaging experiment. The data are collected
on a Cartesian raster during the time period labeled t2,
and in the presence of a y-gradient. Prior to this, a brief x-gradient
pulse has been applied to create a magnetization grating in the
x-direction. The collection period therefore corresponds to the
red rays in the reciprocal space picture at right, and reach individual
ray is collected during a separate experiment. The length of
t1 is systematically varied to achieve the
desired offset along the kx axis.
Notice that the imaging experiment contains two fundamentally different times, a phase encoding interval (t1 during which no data are acquired) and a frequency encoding interval (during data acquisition). These two times permit the separate encoding of the two interactions - the gradients in the two orthogonal directions - and thus allow all of k-space to be sampled. The image is the 2-D Fourier transform of the collected data.
The gradient evolution during the phase encoding interval can be carried out in two fashions, the gradient strength can be kept constant and the time incremented, or the time can be kept constant and the gradient strength incremented. The second, called spin-warp imaging, has advantages since the extent of the evolution due to chemical shift or other non-gradient interactions is kept constant and these then appear solely as a signal attenuation factor. The resultant point spread function for a constant encoding time is an attenuated delta function (neglecting the contribution from sampling).
There are a wide range of imaging sequences and we will not attempt to review these here, they all include the general features shown above. The two dimensional experiments can be extended to three dimensions by encoding the third direction as a second phase encoded axis.
Slice Selection
Recording a full three dimensional image is often not the most
economical approach to imaging and slice selection can be achieved
by taking advantage of the frequency offset dependence of RF excitation.
Looking back at the Bloch equations, Eq. [9], for an on resonance
RF pulse (Dw=0) the RF field is along
the x-axis and hence the evolution of the spins is a simple rotation
about the x-axis. However as Dw increases,
then the dynamics become more complex and are most easily visualized
by considering an "effective" field that is the vector
sum of the RF field along the x-axis and the off-resonance field
along the z-axis. The dynamics are still a simple rotation about
this effective field, but the motion of the magnetization vector
now describes a cone rather than a plane. The result is that
as the frequency offset is increased the angle of the effective
field to the z-axis decreases and eventually the RF pulse has
very little influence. The key to slice selection then is to
apply a relatively weak RF pulse in the presence of a strong gradient,
so that the frequency offset is spatially dependent.
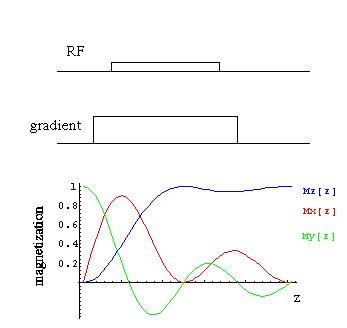
Calculated selective excitation profiles for a weak RF pulse in
the presence of a magnetic field gradient. The pulse length is
set to rotate the on-resonance spins (at the origin) by 90°,
and notice that as the resonance offset increases (with increasing
z) the effective rotation angle becomes smaller and most of the
magnetization remains along the z-axis. For most images, a shaped
RF pulse is employed that creates a square magnetization profile.
There is not a simple linear picture of the dynamics, but various shaped (amplitude modulated) RF pulses have been developed that give well defined square slice selection profiles.
So the overall slice selected 2-D imaging experiment might look
like,
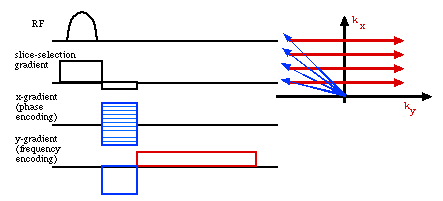
A slice selected 2-D spin warp, gradient echo sequence. Notice
that during the phase encoding time the ky vector is offset so
that both positive and negative values can be sampled. Since
NMR is a coherent spectroscopy, this has the advantage of measuring
the phase. The gradient echo in the slice selection direction
refocuses evolution of the spins during the selective RF pulse.