Lecture Notes on Indexicality
Irene Heim, M.I.T.
1. Simple intensional semantics
1.1. Meaning, truth-conditions, and propositions
"In possible worlds semantics ... the meaning of every sentence is identified with the set of worlds in which it is true. A set of possible worlds therefore is sometimes called a proposition." (Cresswell 1978) Here is the picture that emerges form this and similar introductions to the core ideas of truth-conditional semantics: The basic data of semantics are speakers' judgments about the truth and falsity of actual or hypothetical utterances. Whether a given utterance is true or false depends on two things: the meaning of the sentence uttered, and the possible world in which it was uttered. The meaning of a sentence can therefore be identified with a set of possible worlds, or equivalently, with the characteristic function of such a set, a function from possible worlds to truth values. So the meaning of f is its intension, [[f]]¢. The connection between meanings of sentences and truth values of utterances then is as follows.
(1) An utterance of a sentence f in a possible world w is true if [[f]]¢(w) = 1 and false if [[f]]¢(w) = 0.
The job of compositional semantics is to define [[f]]¢ for arbitrarily complex sentences f. This can be done in a number of technically different ways, but one way or the other, it always amounts to specifying meanings [[a]]¢ for a finite set of lexical items a and formulating composition rules that determine [[a]]¢ for syntactically complex phrases a. (See e.g. Heim & Kratzer, ch.12, for one concrete example.)
1.2. Finer-grained propositions: times and speakers
Can (1) be maintained as it stands? That depends in part on what we mean by a "possible world". If possible worlds are complete possible world histories, then (1) runs into problems as soon as we consider sentences whose truth values vary with time. For example, suppose you knew everything there is to be known about the actual world throughout its development in the past present and future. (Call this world w0.) In particular, you know all about the positions of heavenly bodies at all times in w0, and you also know all about when and where the sentence in (2) has ever been uttered in w0.
(2) The earth is between the moon and the sun.
Suppose, for concreteness, this sentence was uttered twice in the course of actual history, once at a time when the earth was in fact between the moon and the sun, and another time when it wasn't. Given this, and given your knowledge of what the sentence means, you know that the first of these utterances was true and the second one false. But (1) does not permit this possibility. By assumption, both utterances involve the same sentence (2) and occur in the same possible world w0. So whatever function [[(2)]]¢ may be, it either maps w0 to 1 or it maps it to 0. In the first case, (1) says that both utterances are true, and in the second case, that they both are false.
Now there is, of course, the fact that languages (grammars) change, and that what we might call the "same" sentence (at least on some reasonable ways of individuating sentences) has different meanings at different times. If we take this into account, we cannot really speak of the meaning of a sentence simpliciter, but have to relativize this notion somehow (maybe the basic concept is "meaning of a sentence for a given speaker at a given time"). That general point is granted. But does it take care of our example? It arguably does not. The intuitive reason why the first utterance of (2) in our scenario was true and the second one false is not that the sentence changed its meaning in the time in between.
There are two ways to go at this point, and the difference between them is not really important. One possible decision is to take a "possible world" for the present purposes as something without (or with sufficiently short) temporal duration, so that the two utterances of (2) in our example count as taking place in two different worlds. The other option, which we will adopt, is to continue using the term "world" for complete possible histories, and to redefine propositions as functions from world-time pairs to truth values. Instead of (1), we now have (3).
(3) An utterance of a sentence f in a possible world w at a time t is true if [[f]]¢(w,t) = 1 and false if [[f]]¢(w,t) = 0.
This takes care of the problem with sentences like (2), whose truth value depends on the time of utterance. But if we continue thinking along the same lines, we soon see that (3) is still not good enough. What if the same sentence is used in two simultaneous utterances (in the same world)? According to (3), these two utterances could not possibly differ in truth value. But counterexamples to this prediction can be found. Look at (4).
(4) I am sorry.
Imagine you know all the facts of the actual world (w0), and pick a particular time, say Feb. 24, 1989, 2:27:19 pm (call this t0). Now ask yourself whether (4) is true or false in w0 at t0. You probably won't be able to decide. If you are lucky, exactly one person utters I am sorry in w0 at t0. In this case, you could say (4) is true in w0 at t0 if that person is sorry in w0 at t0 and false if s/he isn't. But what if several people in various places of w0 utter (4) at the same time t0, and some of them really are sorry while others are not? Then no truth value can be assigned to (4) in w0 at t0 per se. The best you can do is assign a truth value relative to each choice of speaker.
This suggests that a proposition should be taken to be something still more complicated than a function from world-time pairs. It should be a function that assigns a truth value to each triple of a world, time, and speaker. For instance, the meaning of (4) should be this:
(5) For any world w, time t, and individual x, [[I am sorry]]¢(w,t,x) = 1 iff x is sorry in w at t.
And the new version of the principle that links meanings to the truth-values of utterances should read as follows:
(6) An utterance of a sentence f which is made by x in w at t is true if [[f]]¢(w,t,x) = 1 and false if [[f]]¢(w,t,x) = 0.
It is customary in the literature to refer to the arguments of propositions as indices. In the present theory, an index is thus a world-time-individual triple, whereas in the theory we started out with, it was a world, and in the intermediate theory, it was a world-time pair. In somebody else's theory, it might be yet another kind of thing, for example a quadruple of a world, time, speaker, and place, or a quintuple with a second time as the fifth coordinate. We will presently consider reasons why such further inflation might be called for.
Compositional implementation
Ontology:
(0) W := the set of all possible worlds
T := the set of all times
D := the set of all possible
individuals
Type system:
(1) Basic
types:
De := D
Ds := W«T«D
(the set of world-time-individual
triples)
Dt := {0,1} (the set of truth-values)
Sample lexical entry for a 1-place predicate:[1]
(2) [[sorry]]w,t,x = ly. y is sorry in w at t.
Entry for the first person pronoun I:
(3) [[I]]w,t,x = x.
(Non-trivial) composition rules[2]:
(4) (Ordinary)
Functional Application:
[[a]]w,t,x = [[b]]w,t,x([[g]]w,t,x)
(5) Intensional
Functional Application:
[[a]]w,t,x = [[b]]w,t,x([[g]]¢)
Analysis of example I am sorry:
(7) [[I am sorry]]¢ =
lw,t,x. [[I am sorry]]w,t,x
=
lw,t,x. [[sorry]]w,t,x ([[I
]]w,t,x) =
lw,t,x. [ly.
y is sorry in w at t](x) =
lw,t,x. x is sorry in w at t
The entry we gave for I in a way looks counterintuitive, because it makes no mention of what is intuitively the essential aspect of the meaning of I, viz. that it picks out the speaker. Indeed, nothing at all in the semantics itself tells us in any way that the third coordinate of an intension's argument stands for the speaker. As far as the lexical entry in (3) goes, [[I]]w,t,x is defined regardless of whether x says anything in w at t, or whether x is even the sort of entity capable of talking and thinking. Isn't that a problem? No. The connection between the third member of the triple and the role of speaker of an utterance is established as part of the definition of "truth of an utterance". Therefore it doesn't have to be (and as we will see, shouldn't be) duplicated in the lexical entry of I or any other particular word.
So even though you'll find it
odd that our semantics provides truth values for sentences with respect to very
weird triples -- e.g., a triple consisting of the actual world, the present
moment, and the banana peel here on my desk -- this oddity is harmless. When we consider the empirical
predictions of our semantics, we only care about whether it matches our
intuitions regarding the truth and falsity of (actual or hypothetical)
utterances, and so the only triples <w,t,x> which will interest us as
arguments for the intension of a given sentence f
will be those for which x happens to utter f
in w at t. (This is not strictly true for
utterances of more complex sentences which contain modal and temporal
operators. As we will see shortly,
in the calculation of truth conditions for such utterances it will be crucial
to look at certain triples <w,t,x> where x doesn't utter anything in w at
t.)
1.3. Do we need further coordinates?
We observed that I always refers to the utterer. In the same way, you refers to the addressee, and here to the place of utterance. Shall we treat these items by expanding indices further, as we did for I? This would imply another redefinition of type s and adjustment of the definition of utterance-truth, together with lexical entries as illustrated below.[3]
(11) An utterance of a sentence f which is made in w at t by x in location z and addressed to y is true iff [[f]]¢(w,t,x,y,z) = 1.
(9) Ds := W«T«D«D«D
(10) [[lazy]]w,t,x,y,z
= lu. u is lazy in w at
t.
[[live]]w,t,x,y,z = lu. lv. v lives in u in w at t.
[[I]]w,t,x,y,z = x.
[[you]]w,t,x,y,z = y.
[[here]]w,t,x,y,z = z.
With appropriate routine adjustments to the composition principles, we could then derive sentence meanings like (12a,b) and predictions about utterance truth like (13a,b).
(12) (a) [[you are lazy]]¢ = lw,t,x,y,z. y is lazy in w at t.
(b) [[I live here]¢ = lw,t,x,y,z. x lives
in z in w at t.
(13) (a) If x
utters you are lazy to y in w at t,
then
x speaks truly iff y is lazy in w
at t.
(b) If
x utters I live here at location
z in w at t,
then
x speaks truly iff x lives in z in
w at t.
Chances are that yet more coordinates would have to be added to the index as we treat further vocabulary items.[4]
But do we really need all these separate coordinates? A natural alternative strategy comes to mind, namely to exploit the fact that certain parameters can be defined in terms of others. For instance, given an utterance world w, a speech time t, and a speaker x, the place of the utterance is simply that location which x occupies in w at t. Likewise, the addressee is that individual whom x addresses in w at t. So why don't we keep Ds = W«T«D and the definition of utterance truth as in (6), and write the lexical entries as follows:
(14) [[lazy]]w,t,x
= lu. u is lazy in w at
t.
[[live]]w,t,x = lu. lv. v lives in u in w at t.
[[I]]w,t,x, = x.
[[you]]w,t,x = that individual whom x addresses in w at
t;
undefined
if there is none.
[[here]]w,t,x = that place which x occupies in w at t.
For our current two example sentences, we then obtain the propositions in (15a,b).
(15) (a) [[you are lazy]]¢ =
lw,t,x. the one whom x addresses in w at t is
lazy in w at t.
(b) [[I live here]¢ =
lw,t,x. x lives in w at t in the place which
x occupies in w at t.
These are different propositions from the ones in (12a,b), but when we apply the utterance truth definition in (6) to them, we get the desired predictions in (13a,b) all the same.
Attractive though this parsimonious strategy may be, it leads straight into a serious problem.[5] This is the topic of the next section.
2. A problem
Assuming the entries for I and here in (14), consider the meaning we derive for sentence (16).[6]
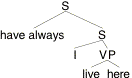
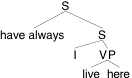
(16) I have always lived here.
Let's treat have-always as a single word that combines with sentences here. It should have the lexical entry (17), and the LF should be approximately (18).
(17) [[have-always]]w,t,x = lp.[for all t' before t: p(w,t',x) = 1].
(18)
We calculate the following intension:
(19) [[(18)]]¢ =
lw,t,x. 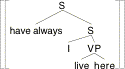 w,t,x =
w,t,x =
lw,t,x. [for all t'
before t: ![]() w,t',x
= 1] =
w,t',x
= 1] =
lw,t,x. [for
all t' before t: [[live]]w,t',x([[here]]w,t',x)([[I]]w,t',x)] =
lw,t,x. [for
all t' before t:
x
lives in w at t' in the place which x occupies in w at t']
So, for instance, if John utters this sentence in the actual world right now, we predict that he speaks the truth just in case it was true at every past time that he lived in whatever place he was occupying then.
But these are not the intuitive truth-conditions of this utterance. Suppose, for instance, John lives in Somerville now, but lived in Los Angeles last year, and in each of these places he never left home. Then his utterance (which he is making now in his home in Somerville) is intuitively false. His audience would justly reply: "No, that's not true. You haven't always lived here. You used to live in Los Angeles." But our analysis predicts it to be true. How so? Because it is the case that John always lived in the place he was occupying at the time.
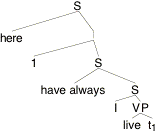
What went wrong? It might be suggested that in (18) we gave our example sentence the wrong LF. We should have QRed here to give it wider scope than have-always, as in (20).
(20)
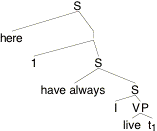
Indeed, if we calculate the proposition expressed by this alternative LF, the result is more promising:
(21) [[(20)]]¢ =
lw,t,x [for
all t' before t:
x
lives in w at t' in the place which x occupies in w at t]
Exercise: Prove this. (To do so, you have to integrate variables and variable binding into the semantics. But that's a routine task.)
(21) correctly implies that the John of our story above speaks falsely when he utters (20): There are past times - namely those when he lived in L.A. - at which he did not live in the place of his present utterance. And these times falsify the truth condition in (21).
This result, however, doesn't suffice to vindicate our semantic analysis. For even if (20), with its intuitively adequate truth-conditions, is one of the grammatical LFs for sentence (16), there is no plausible reason why (18) shouldn't be an available LF as well. So at best we are predicting that the sentence is ambiguous between the two readings in (19) and in (21). But in fact it isn't ambiguous. There just isn't any reading like (19) for this English sentence. And there is no pragmatic implausibility inherent in such a meaning that might explain its absence, nor any known syntactic principle that we might invoke to exclude its LF.
The only way to save our theory at this point would be by means of a stipulation: here obligatorily takes wider scope than any temporal or modal operator. This rule apparently even takes precedence over any constraints that syntactic structure might otherwise impose on scope possibilities. Even the most deeply embedded occurrences of here seem to take maximal scope:
(22) Mary always sends me many things that I never mention to anyone who works here.
(23) I am usually neither here nor where they need me.
This is not an attractive theory. The complete insensitivity to syntactic structure that we observe in this putative wide-scope tendency of here suggests that scope is not, after all, what is really at issue here.
How else can we avoid the prediction of inadequate truth-conditions? Well, one solution turns out to be to introduce a separate place-coordinate in the index after all. In other words, sacrifice parsimony and return to lexical entries like those in (10), repeated here together with an appropriate trivial revision of the lexical entry for have-always.
(24) [[live]]w,t,x,y,z
= lu. lv. v lives in u in w at t.
[[I]]w,t,x,y,z = x.
[[here]]w,t,x,y,z = z.
[[have-always]]w,t,x,y,z = lp.[for
all t' before t: p(w,t',x,y,z) = 1]
Let's use these entries to interpret our original, simpler, LF in (18). Here is what we get:
(25) [[(18)]]¢ =
lw,t,x,y,z.[for
all t' before t: x lives in z in w at t'].
When we apply the definition of utterance-truth in (11), this yields the correct prediction: John, who utters (16) right now at his home in Somerville, speaks truly iff it holds of every time in the past that John lived then in the place he is occupying now. Since this does not hold of the times when he lived in L.A., he speaks falsely.
Considerations analogous to those we have presented for here can be adduced to justify a number of additional coordinates in the index, including the addressee coordinate, and also a second time coordinate (the latter argued for originally by Kamp 1971). See homework problem below.
3. Point of evaluation versus context of utterance
Kaplan, Stalnaker, and others have felt the need for a more principled account of the nature of indices and their role in determining the truth values of utterances. They have argued that indices as currently conceived lump together two very different determinants of truth value that are better kept distinct.
The traditional picture in intensional semantics, as we sketched it in section 1.1, was that the truth value of a given utterance is determined by two factors: first, it depends on what the sentence uttered means, and second, on what the world in which the utterance is made happens to be like. So if somebody is unable to tell whether a given utterance is true or false, this could be due either to semantic ignorance or to factual ignorance (or, of course, to a combination of both). For instance, if I don't know the truth value of an utterance of (26),
(26) John's sweater is mauve.
this could be because I haven't seen John's sweater and therefore don't know what color it is (factual ignorance), or else it could be because I am not familiar with the meaning of the color term 'mauve' (semantic ignorance)[7].
The distinction between these two sources of possible ignorance is transparent in our semantics in the way in which extensions are assigned to expressions. First, the semantics of the language (lexicon + composition rules) assigns to each expression a a meaning [[a]]¢, then this is applied to an index to yield an extension. Semantic ignorance amounts to not knowing which interpretation function [[...]]¢ to apply, and factual ignorance to not knowing which index to apply it to. We can visualize this set-up in a diagram:
(27) expression
a
–¨ meaning
semantics =
intension [[a]]¢
–¨ extension [[a]]¢(w,t,x...)
index
<w,t,x,...>
Kaplan and Stalnaker now argue that there are really not just two, but three, different causes for ignorance of truth value. Stalnaker puts it as follows (1970: 180).
"Suppose you say "He is a fool" looking in the direction of Daniels and O'Leary. Suppose it is clear to me that O'Leary is a fool and that Daniels is not, but I am not sure who you are talking about. Compare this with a situation in which you say "He is a fool" pointing unambiguously at O'Leary, but I am in doubt about whether he is one or not. In both cases, I am unsure about the truth of what you say, but the source of the uncertainty seems radically different. In the first example, the doubt is about what proposition was expressed, while in the second there is an uncertainty about the facts."
Neither of Stalnaker's two cases here involves semantic ignorance. This would be yet a third possibility: I might be unsure about the truth of what you say because my English is deficient (perhaps I haven't learned the word 'fool' yet) Ð even if I know exactly who you are referring to and whether or not he is a fool. Altogether, then, there are three possibilities, and Stalnaker proposes to make this transparent by adopting a model of semantic interpretation that may be diagrammed as follows:
(28) expression a
–¨ meaning
semantics = character [[a]]$
–¨ intension [[a]]$(c)
context of utterance c
–¨ extension [[a]]$(c)(i)
point of evaluation i
Although our terminology here is different (see right below), this diagram represents what Stalnaker proposes in the following passage (p. 179):
"The scheme I am proposing looks roughly like this: the syntactical and semantic rules for a language determine an interpreted sentence or clause; this, together with some features of the context of use of the sentence or clause determines a proposition; this in turn, together with a possible world, determines a truth-value. An interpreted sentence, then, corresponds to a function from contexts into propositions, and a proposition is a function from possible worlds into truth-values."
The term "character" is Kaplan's and corresponds to Stalnaker's "interpreted sentence", or more generally (for phrases of categories other than S) "interpreted expression." Here is a rough definition.[8]
(29) The character [[a]]$ of an expression a is a function from utterance contexts to intensions of the appropriate type (where the appropriate type depends on the syntactic category of a).
The character of a sentence, for instance, is a function from contexts to propositions, whereas the character of a (non-quantificational) DP is a function from contexts to individual concepts. Characters are now what the semantic component of a language has to define compositionally for all its LFs.
What is an (utterance) context (= "context of use" in Stalnaker)? Let's take it to be a triple <w,t,x> ë W«T«D such that x makes an utterance in w at t. When 'c' stands for such a triple, we write 'wc', 'tc', and 'sc' to refer to its 1st, 2nd, and 3rd coordinates. These are the world in which the utterance takes place, the time at which it occurs, and the speaker who makes it, respectively. Other features of the utterance can be defined in terms of these three (see above). For instance, the audience (if any) is whoever sc addresses in wc at tc; the place of utterance is the place which sc occupies in wc at tc; etc. The contexts are a proper subset of W«T«D: every context is a triple in W«T«D, but not every triple in W«T«D is a context. For instance, a triple consisting of the actual world, a moment in the year 1,500 B.C., and me, is not a context, because I didn't actually utter anything then.
A character [[a]]$, applied to a context c, yields an intension [[a]]$(c). In the special case that Stalnaker concentrates on, where a is a sentence, [[a]]$(c) is the proposition that a expresses in c.
An intension, according to the diagram, is a function from points of evaluation to extensions. A point of evaluation is an index, and what exactly this consists of remains to be decided. For Stalnaker, it 's just a possible world. We'll take it to be a world-time pair for the time being, but will attempt a more principled approach to the decision below.[9] The term "point of evaluation" also comes from Kaplan. Stalnaker doesn't have any neutral term for whatever it may be that an intension takes as its argument.[10]
In the light of the diagram (28), consider again Stalnaker's example He is a fool and the three different reasons why I might not know whether a given utterance of this sentence is true.[11] Case 1: If I don't understand English (or fail to realize that this is the language you are speaking), I won't even manage to get from the sentence He is a fool to its character [[he is a fool]]$. Case 2: Supposing that I do make it this far, I might still lack relevant information as to which of various possible utterance contexts we are in. For instance, I may be unsure whether we are in a context in the set C1 := {c: sc is pointing at Daniels in wc at tc}, or rather in a context in the set C2 := {c: sc is pointing at O'Leary in wc at tc}. Unfortunately, for all c ë C1, [[he is a fool]]$(c) is the proposition (call it p1) which is true in exactly those worlds where Daniels is a fool; whereas for any c ë C2, [[he is a fool]]$(c) is the proposition p2 which is true in exactly those worlds where O'Leary is a fool. p1 p2; so in this case, I didn't manage to determine the intension. Case 3: Suppose, finally, that I did see that Daniels was being pointed at rather than O'Leary, and thus I know that we are in a context in C1 and not in one in C2. So I know that the proposition expressed was p1. Still I may not know whether the utterance was true, because for all I know, we might equally well be in a world where Daniels is a fool, as in a world where he isn't. So I don't know enough about what is the appropriate point of evaluation to get from the proposition p1 to an extension (truth value) for the utterance.
Implicit in the discussion of this example was an assumption about how we define 'truth of an utterance' in this new framework. Here is the explicit definition:
(30) If a sentence f is uttered in an utterance context c, then this utterance is true iff [[f]]$(c)(wc,tc) = 1.
As this definition shows, as long as we are concerned just with the truth or falsity of a given utterance, we consider the same possible world and time in dual roles: as utterance world/speech time and as point of evaluation. Still, we cannot simplify the theory by just collapsing these two. That is the main point of Stalnaker's article, and we will now take a closer look at one of his arguments.
4. An argument for the "extra step"
We have already seen one possible motivation for the more complex picture in (28) over the simpler one in (27): it arguably allows us to capture a real intuitive difference between not knowing what was said and not knowing whether what was said was true. Stalnaker mentions a few more reasons. For instance, he claims that the new notion of a proposition expressed in a context is needed to provide a natural characterization of the relation between questions and their answers (p. 179):
"If O'Leary says 'Are you going to the party?' and you answer, 'Yes, I'm going', your answer is appropriate because the proposition you affirm is the one expressed in his question. On the simpler analysis, there is nothing to be the common content of question and answer except a truth value. The propositions are expressed from different points of reference, and according to the simpler analysis, they are different propositions. A truth value, of course, is not enough to be the common content. If O'Leary asks 'Are you going to the party?' it would be inappropriate for you to answer, 'Yes, snow is white.'"
Let's spell out the analysis of this dialogue in each of the two approaches in more detail. We haven't dealt with questions so far, but we may assume here for simplicity that the semantic value of a yes-no question minus the question mark is the same as that of the corresponding declarative. The question mark then somehow indicates the interrogative illocutionary force.[12] In our example, we are dealing with a sequence of two utterances. Utterance #1 is spoken in a world w0, at a time -- say 12/31/1988, 1pm, by O'Leary, addressed to another person (= the reader of Stalnaker's paper), and involves the sentence You are going to the party tonight + ? Utterance #2 is spoken in w0, at a time shortly after utterance #1 -- say 12/31/1988, 1:00:04pm, by that other person, addressed to O'Leary, and involves the sentence I am going to the party tonight. (I fixed up Stalnaker's sentences a little to avoid irrelevant complications.)
Now let's first take the old approach, as in diagram (27). The semantics of English may be assumed to make the following assignments to our two sentences:
(31) [[you are going to the party tonight]]¢ is the function
[lw,t,x,y. y goes to the party in w on
the evening of the day which includes t].
(32) [[I am going to the party tonight]]¢ is the function
[lw,t,x,y. x goes to the party in w on
the evening of the day which includes t].
We are taking indices (Stalnaker calls them "points of reference") to be quadruples of a world, a time, and two individuals, where the two individuals stand for the speaker and the audience respectively.[13] (This would be written into an appropriate definition of "truth of an utterance" along the lines of (11) above.) The indices for the two utterances in our example are these:
(33) index for utterance #1:
i1 = <w0,
12/31/1988/1pm, O'Leary, the other person>
index for utterance #2:
i2 = <w0,
12/31/1988/1:00:04pm, the other person, O'Leary>
What do the two utterances have in common? It is not the case that [[I am going to the party tonight]]¢ is identical to either [[you are going to the party tonight]]¢ or its negation, as (31) and (32) clearly show. So on the level of intensions, utterance #1 and utterance #2 have nothing in common. At best we can say that they are alike on the level of extensions: [[I am going to the party tonight]]¢ applied to the index i2 yields the same truth value as [[you are going to the party tonight]]¢ applied to the index i1, as the following calculation shows.
(34) [[I am going to the party tonight]]¢(w0, 12/31/1988/1:00:04pm, the other person, O'Leary) = 1
iff [by (32)]
the other person goes to the party in w0 on the evening of 12/31/1988
iff [by (31)]
[[you are going to the party tonight]]¢(w0, 12/31/1988/1pm, O'Leary, the other person) = 1.
However, as Stalnaker points out, such agreement of truth values is not enough to distinguish coherent dialogues like this one from incoherent ones like: Are you going to the party tonight? -- Snow is white. If it so happens that the other person is going to the party , then the intension of this "answer", evaluated at the index i2, likewise agrees in truth value with the intension of the question evaluated at the index i1.
Now let us analyze the same example in the new approach that involves the extra step, as diagrammed in (28). This time, the semantics of English provides an assignment of characters. Concretely, we may assume the following interpretations for our two sentences[14]:
(35) [[you are going to the party tonight]]$ is that function F such
that,
for any context c and any point of evaluation wëW:
F(c)(w) = 1 iff the one whom sc addresses in wc at tc goes to the
party in w on the evening of the day which includes tc.
(36) [[I am going to the party tonight]]$ is that function
G such that,
for any context c and any point of evaluation wëW:
G(c)(w) = 1 iff sc goes to the party in w on the evening of
the day which includes tc.
The contexts for the two utterances in our example are these (where w0 is by assumption a world in which O'Leary addresses the other person at 12/31/1988/1pm, and the other person addresses O'Leary at 12/31/1988/1:00:04pm).
(37) context for utterance #1: c1 = <w0, 12/31/1988/1pm, O'Leary>
context for utterance #2: c2 = <w0, 12/31/1988/1:00:04pm, the other person>
Again we ask what the two utterances have in common. Nothing on the level of characters: as (35) and (36) make clear, [[you are going to the party tonight]]$ [[I am going to the party tonight]]$. But consider the level of intensions. If we apply the characters of each utterance to their respective utterance contexts, we find that [[you are going to the party tonight]]$(c1) = [[I am going to the party tonight]]$(c2), as the following calculation shows.
(38) For any wëW:
[[I am going to the party
tonight]]$(w0, 12/31/1988/1:00:04pm, the other person)(w) = 1
iff
[by (36)]
the
other person goes to the party in w on the evening of 12/31/1988
iff
[by specification of w0]
the
one whom O'Leary addresses in w0 at 12/31/1988/1pm goes to the
party in w on the evening of 12/31/1988
iff
[by (35)]
[[you are going to the party tonight]]$(w0, 12/31/1988/1pm, O'Leary)(w) = 1.
Had the answer been Snow is white, no such identity of expressed propositions would have obtained. Indeed, the following generalization seems to capture the intuitive difference between appropriate and inappropriate answers:
(39) Let f? be a (yes-no) interrogative sentence, y a declarative sentence, and c and c' two contexts such that f? is uttered in c and y is uttered in c'. Then the utterance of y in c' is a direct affirmative answer to the utterance of f? in c iff [[y]]$(c') = [[f]]$(c). Similarly, the utterance of y in c' is a direct negative answer to the utterance of f? in c iff [[y]]$](c') = li.[[f]]$(c)(i) = 0.[15]
(39) predicts that Snow is
white is not a direct answer (either
affirmative or negative) to Are you going to the party? (39)
also predicts that an answer that has the same character as the question is
often inappropriate, e.g. the deviance of Are you going to the party? -- Yes, you are going.
We have seen, then, that the new framework of semantic interpretation makes it easy to pinpoint what questions have in common with their (direct, appropriate) answers. In the old framework, this was not as easy. This is not to say that it would be completely impossible to define the question-answer relation in that framework. For instance, one could have defined it as follows:
(40) Let f? be a (yes-no) interrogative sentence, y a declarative sentence, and <w,t1,x,y> and <w,t2,y,x> two indices such that f? is uttered in w at t1 by x to y, and y is uttered in w at t2 by y to x. Then the utterance of y is a direct affirmative answer to the utterance of f? iff for all w'ëW: [[f]]¢(w',t1,x,y) = [[y]]¢(w',t2,y,x). (Similarly for "direct negative answer".)
However, this definition treats some coordinates of the index differently from the others. There is universal quantification over the world-coordinate, while the other coordinates are kept fixed. In effect, then, (40) imposes an asymmetry between two groups of coordinates that is intuitively just the asymmetry between context and point of evaluation in the new approach. So in a way, (40) proves Stalnaker's point rather than undermining it: if one wants to characterize the question-answer-relation in the old approach, one must implicitly draw just the distinction between two types of index-coordinates that is transparent in the new approach.
There are a number of other relations between utterances that raise very similar issues as the question-answer relation, for instance: What does it mean for two interlocutors to "agree" or to "disagree"? What does it mean for a speaker to "contradict herself"? Here too, the relevant relations hold neither on the level of characters nor on the level of extensions, but rather on the intermediate level of intensions. If I say I am smarter than you and you say I am smarter than you, we are disagreeing, even though we have employed the same sentence and hence the same character (and the same intension under the old approach!). The reason is that the intensions (as construed in the new approach) that are expressed by our respective utterances in their respective contexts are mutually incompatible propositions.[16] Similarly, if I say now: I am thirty-nine now, and a year from now again: I am thirty-nine now, I contradict myself. These concepts of (dis)agreement and contradicting oneself can be used to make the same point that Stalnaker makes about the question-answer relation: they are captured more naturally in the new approach than in the old one.
Homework problem
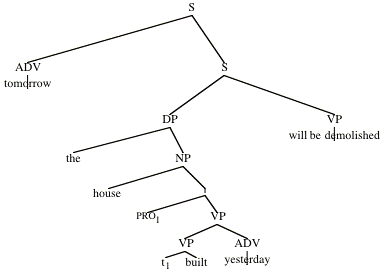
Consider the sentence
(1) Tomorrow, the house built yesterday will be demolished.
For concreteness, assume the LF in (2):
(2)
Suppose we are working in a traditional intensional semantics (with a "one-step" set-up as in diagram (27)), and our indices are world-time pairs. The following lexical entries for the adverbs yesterday and tomorrow would seem reasonable then.[17]
(3) [[tomorrow]]w,t =
lp<s,t>. [there
is a time t' on the day after t such that p(w,t') = 1]
(4) [[yesterday]]w,t =
lp<s,t>. [there
is a time t' on the day before t such that p(w,t') = 1]
For the other items in the example, use the following standard lexical entries:
(5) [[house]]w,t = lx. x is a house in w at t.
(6) [[built]]w,t = lx. somebody builds x in w at t.
(7) [[demolished]]w,t = lx. somebody demolishes x in w at t.
(8) [[the]] = lf. the unique x such that f(x) = 1.
The remaining items (in particular will and be) are assumed to be vacuous. Also pro is vacuous, though not its index (see H&K, ch. 8, sec. 5, for this treatment of XPs that modify nouns[18]).
The assignment consists of four parts. The first part is concerned with identifying a problem with the treatment just sketched, and the remaining three parts with various responses to this problem.
(i)
Show that the assumptions outlined above lead to an inadequate interpretation for sentence (1). The best way to do this is to imagine a concrete world w0 and time t0 such that (1) uttered in w0 at t0 is intuitively true in w0 at t0, but predicted by the above analysis to be false in w0 at t0.
(ii)
Show that the truth conditions come out right if (1) is assigned a different LF, namely one in which the DP the house built yesterday takes widest scope. (None of the other assumptions are to be revised to obtain this result.)
(iii)
Returning to the assumption that the LF of (1) is (2), can the problem be solved by admitting more complicated indices? I.e., will it help to include further coordinates besides the world and time coordinates employed above? [Hint: look at the end of section 2, pp. 7 - 8.]
(iv)
How would Stalnaker 1970 approach the problem? Suppose that we introduce the distinction between character and intension (i.e., switch to the "two-step" model), and assume that the compositional semantics defines characters.
For concreteness, assume a system in which semantic values are extensions, and the semantic value of an expression depends (in the general case) on a context, a point of evaluation, and a variable assignment. So we put three superscripts on the semantic-value brackets: [[a]]c,i,a, where c is a context, i an evaluation point, and a an assignment. We assume here that contexts are triples in W«T«D (where wc, tc and sc are defined as the 1st, 2nd, and 3rd member of c respectively), and that evaluation points are pairs in W«T (where wi and ti are defined as the 1st and 2nd member of i respectively). As usual, we may omit any one of these superscripts when the extension of a happens to be invariant with respect to it. Typical lexical entries in this framework will look like this.
(9) [[I]]c = sc.
(equivalently: for all assignments
a and all evaluation points i: [[I]]c,i,a = sc.)
(10) [[lazy]]i =
lx. x is lazy in wi at ti.
(equivalently: for all assignments
a and all contexts c:
[[lazy]]c,i,a = lx. x is lazy in wi at ti.)
In this system, the concepts of "intension" and "character" receive the following definitions:
(11) For any assignment a and context c, [[a]]¢c,a := li.[[a]]c,i,a.
[[a]]¢c,a is called the intension of a at c under a. 'i'
here is a variable for evaluation points.
(12) For any assignment a, [[a]]$a := lc.[[a]]¢c,a.
[[a]]$a is called the character of a under a. 'c' here
is a variable for contexts.
Your task now is to spell out the pertinent lexical entries and composition principles for the treatment of our example (=the LF in (2)), to apply them, and to show how you predict intuitively adequate truth-conditions.
5. Diagnosing indexicals in natural language
Stalnaker, Kaplan, and others have argued that the two-step model of semantic interpretation is indispensable for the proper semantic analysis of words like I, here, now in English and their counterparts in other languages. We now want to take a closer look at their argumentation, with an eye to highlighting the empirical claims about natural language that enter into it and the linguistic data that they aim to explain.
Before we get started, let's define a few technical terms.[19]
(1)(a) An
expression a is directly referential,
(equivalently: a is a rigid
designator) iff its character satisfies the following condition:
For any context c and evaluation-points i and i': [[a]]$(c)(i) = [[a]]$(c)(i').
(b) a is an indexical iff a is directly referential and there are contexts c and c' such that [[a]]$(c) [[a]]$(c).
So a directly referential expression or rigid designator is an expression whose extension does not depend on the evaluation point. Its extension may vary from one context to the next, in which case it is called an indexical, but for a given context, it never varies with the choice of evaluation point.
The claim about I, here, etc. that we are going to examine can now be put as follows: these words are indexicals (directly referential, rigid designators). What this means in technical terms is not hard to grasp. For an illustration, consider the following two hypothetical lexical entries for the word here.
(2) For any
context c = <wc,tc,sc>
and any point of evaluation i = <wi,ti>:
[[here]]c,i = the place that sc
occupies in wc at tc.
(3) For any context c
= <wc,tc,sc> and any
point of evaluation i = <wi,ti>:
[[here]]c,i = the place that sc
occupies in wi
at ti.
The difference is in the bold-faced parts: where (2) refers to context-world and context-time, (3) refers instead to evaluation-world and evaluation-time. If we apply the definition in (1), we see that (2) is compatible with the claim that here is an indexical, but (3) is not. So the thesis that here is an indexical implies that (3) cannot be the correct lexical entry for it, whereas (2) might be. (This thesis by itself, of course, doesn't imply that the specific entry in (2) must be the right one. It allows, in principle, many other meanings that we could assign to here. But it does constrain the possibilities, ruling out, e.g., the entry (3).)
But while the technical distinction between indexicals and non-indexicals is plain enough, the task of telling them apart by empirical criteria is not at all simple. What difference does it make in terms of predicted linguistic data whether we adopt (2) or (3)? How do we recognize an indexical when we are out there in the field?
To see that the issue is non-trivial, let's begin with a negative point: We can not determine whether a word is an indexical if we merely examine the truth-conditions of simple sentences containing this word. For every indexical lexical entry that is consistent with this kind of evidence, there is a minimally different non-indexical entry that also is. We can illustrate this with the pair of competing hypotheses in (2) and (3). Let us look at a sentence like (5).
(5) John is here.
To find out what this sentence means, we will utter it (or imagine it being uttered) in various (real or hypothetical) situations and will ask our native speaker consultants to judge these utterances as true or false. The results of this experiment cannot possibly help us decide between (2) and (3). Why not? Let us work out what each hypothesis (together with fixed accompanying assumptions) predicts. In each trial of the experiment, we are looking at a particular utterance of sentence (5) in a particular context. Let's refer to this context as c, and to our utterance of (5) in c as u(5),c. Now we apply the definition for "truth of an utterance" (repeated in (6) from section 3, (30)), as well as the pertinent composition principles and entries for morphemes other than here, and we arrive at the schematic prediction in (7).
(6) If a sentence f is uttered in an utterance context c, then this utterance of f in c is true iff [[f]]$(c)(wc,tc) = 1.
(7) u(5),c is true
iff the place that John occupies in wc at tc is [[here]] c,<wc,tc>.
Now if we assume the entry in (2), we get [[here]] c,<wc,tc> = the place that sc occupies in wc at tc. And if we assume the entry in (3), we get just the same. So whichever we choose, we predict that u(5),c is true just in case in wc at tc, John and sc occupy the same place.
This collapse of predictions is due to a general feature of the definition in (6) which we have already noticed: When it comes to determining the truth-value of an utterance, we employ the utterance-world and utterance-time in two roles at once: as parameters of the context and as parameters of the evaluation point.
So how could we possibly get evidence bearing on the choice between (2) and (3), or between similar minimal pairs of an indexical and a non-indexical entry for a given word? We will have to elicit other kinds of judgments (not just truth-value judgments), consider more complex sentences, and reason in a more round-about way.
5.1 Test 1: common-ground invariance
The passage from Stalnaker's paper that we quoted at the beginning of section 3 suggests the following thought experiment: Imagine O'Leary utters (5) to you (at a time t0) and you don't know where O'Leary is (at t0). Imagine, for instance, he is speaking to you on the phone, and you don't know whether he is calling from his home or his office. This means that, for all you know, you may be confronted with either one of two possible utterances (actually, each of these represents an infinite set of possible utterances which differ further from each other in respects irrelevant here):
(8) u1: an utterance of sentence (5), by O'Leary, at time t0, in a world w1 in which O'Leary is at home at t0.
u2: an utterance of sentence (5), by O'Leary, at time t0, in a world w2 in which O'Leary is in his office at t0.
Now according to hypothesis (3), u1 and u2 express the same proposition p:
(9) p = lw,t [in w at t, John is where O'Leary is in w at t]
If this hypothesis is correct, then despite your uncertainty as to whether you are dealing with u1 or u2, you should feel that you have understood what O'Leary has told you (though you don't know whether it's true). -- Hypothesis (2), by contrast, predicts that u1 and u2 express different propositions, namely q1 and q2 respectively:
(10) (a) q1 = lw,t [in w at t, John is at O'Leary's home]
(b) q2 = lw,t [in w at t, John is at O'Leary's office]
If this hypothesis is correct, you ought to feel that you haven't quite understood what O'Leary told you, and you should be inclined to request a clarification ("Where is 'here'? Where are you calling from?"). Does intuitive judgment here favor hypothesis (2)? Arguably yes.
The general principle we have applied in this thought experiment might be stated as follows: In felicitous communication, the hearer can uniquely identify the proposition expressed by the speaker. This means that in all the possible contexts which, for all the hearer knows, the utterance might be located in, it picks out the same intension.[20] This principle says that, in felicitous communication, the proposition expressed by each utterance does not vary from one context to the next within the common ground. (By the "common ground" here we mean the set of possible utterance contexts which, for all the speaker and hearer can tell at this point in the conversation, might be the context they are in.) I will call this the principle of common ground invariance.
Given this principle, we have here a first argument for the superiority of the indexical analysis of here over its non-indexical competitor. The indexical analysis predicts that different propositions are expressed depending on whether O'Leary is speaking at home or in the office. The non-indexical analysis predicts that the same proposition is expressed. So the principle of common ground invariance together with the indexical lexical entry predicts that the utterance is somehow infelicitous if both kinds of contexts are in the common ground. Whereas the same principle together with the non-indexical entry predicts no violation. Everything else being equal, therefore, the indexical analysis contributes to an account of an actual judgment of infelicity, whereas the non-indexical analysis doesn't.
5.2. Test 2: semantic relations between utterances
Let's try a second thought experiment, this one based on the remarks in Stalnaker (1970) that we elaborated in section 4. Suppose I am looking for a good place for a potted hibiscus, and I am going from room to room in my house. In the living room window bay, I say to myself: "Here is the sunniest spot." Then, when I get to the kitchen window, I say again: "Here is the sunniest spot." Did I agree with myself or contradict myself? Intuitive judgment is that I contradicted myself.
Within the 2-step model of interpretation, we can give a simple characterization of the contradiction relation between utterances, as follows: The utterance of sentence f in context c contradicts the utterance of sentence y in context c' iff there is no possible evaluation point i which is mapped to 1 both by the proposition [[f]]$(c) and the proposition [[y]]$(c').[21] In other words, the contradiction-relation between utterances reduces to the contradiction-relation between the propositions expressed by them.
Now let's see whether our example of a pair of intuitively contradictory utterances turns out to be an instance of this definition. Well, this depends again on which of the two entries for here we assume. If we apply the non-indexical entry (3), both utterances express the proposition li [the place which Irene occupies in wi at ti is sunnier in wi at ti than any other place]. So they do not contradict each other in the technical sense. But if we employ the indexical entry (2), then the first utterance expresses the proposition li[Irene's living room bay is sunnier in wi at ti than any other place], and the second utterance expresses the proposition li[Irene's kitchen window is sunnier in wi at ti than any other place]. These two propositions can never both be true at a given i, so the two utterances do qualify as contradicting each other in the sense of our definition. So again, we have a roundabout argument for the indexical analysis: everything else being equal, it predicts the intuitive judgment that there is a contradiction, while its non-indexical competitor does not.
Similar arguments could be based on other semantic relations between utterances, e.g., the question-answer relation that we defined in section 4.
5.3. Test 3: content anaphora
Words like that, this, it (and null complement anaphora) can apparently be used to refer to the propositions expressed by utterances in the previous discourse. This being so, the truth-conditions of the utterances containing such anaphors may indirectly reveal something about the propositions expressed by their antecedents.
Consider the dialogue in (11).
(11) A: Hi, I am calling from E39-234. John is here.
B: That I already knew. But I am astonished that you are there. You normally avoid John like the plague, don't you?
What proposition does the that in B's first sentence refer to? Apparently it refers to the proposition that was just expressed by A's utterance of John is here. Now, what proposition is that?
According to one of our hypotheses about here, the non-indexical analysis (3), it is the proposition li[in wi at ti, John is where A is in wi at ti]. So we predict that B is saying that he already knew this proposition. But it is clear from the remainder of his reply that he did not. As he's making explicit, B did not at all know that A and John were in the same place.
According to our other hypothesis about here, the indexical entry in (2), the proposition expressed by A's utterance is the proposition li[in wi at ti, John is in E39-234]. So we predict that B is saying that he already knew this proposition. This indeed is how we understand B, and it is perfectly consistent with his not having known that A and John were in the same place.
So once again, we find that the indexical analysis of here supports an account of an intuitive judgment (here a judgment about the truth-condition of a subsequent utterance), whereas Ð everything else being equal Ð the non-indexical analysis fails to predict that judgment (in fact, predicts a different one). So we have another tentative argument in favor of the indexical entry. This argument depends on a certain analysis of the anaphor that, and it could therefore break down if that analysis were abandoned. Indeed, we have not argued independently for the generalization that that refers to the proposition expressed in the antecedent utterance. Maybe we can tell a different story about how that is interpreted, and on that story we will no longer need the indexical entry of here to account for the truth-conditions of I already knew that. Maybe. But the burden of proof is on the other side now. The generalization about that that we employed is straightforward and apparently consistent with the judgments in those cases where no putative indexicals occur and there is no controversy about which proposition is expressed. If you want to challenge our argument for the indexicality of here, it's your responsibility to propose an equally appealing alternative treatment of that.
5.4. Test 4: scopelessness
Finally we return to our observations about here in section 2 and examine how those might bear on the decision for or against an indexical analysis. There we considered the sentence I have always lived here (see also Stalnaker's sentence I didn't have to be here), and we noted that Ð independently of scope constellations Ð this sentence should not receive an interpretation equivalent to "At every past time t, I lived where I was at t." (Or, for the Stalnaker sentence, an interpretation equivalent to "In some accessible world w, I am not where I am in w.") Let us see how (2) and (3) each fare with respect to this desideratum.
Suppose the sentence I have always lived here, with the LF (16) (repeated from above), is uttered in a context c.
(16)
We want to calculate the condition under which this utterance is predicted true. To do so, we need lexical entries not just for here, but also for I, live, and notably for have-always, as well as composition principles to apply to the phrasal nodes. Let's assume the usual entries for I and live and the usual composition rules of ordinary and Intensional Functional Application. These are, in the current framework (and in abbreviated notation):
(17) (a) [[I]]c,i = sc
(b) [[live]]c,i = lx. ly. [y lives at x in wi at ti]
(18) FA: [[b g]]c,i = [[b]]c,i([[g]]c,i)
(19) IFA: [[b g]]c,i = [[b]]c,i([[g]]¢c)
As for here and have-always, we will not commit ourselves right now except as to their semantic type: [[here]]c,i ë De, and [[have-always]]c,i ë D<st,t>. So the calculation of the truth-condition of (16) uttered in c will look as follows:
(20) The utterance of (16)
in c is true
iff
[[(16)]]c,<wc,tc> = 1
iff
[[have-always]]c,<wc,tc>(li.[[I live here]]c,i) = 1
iff
[[have-always]]c,<wc,tc>(li.[[live]]c,i([[here]]c,i)([[I ]]c,i)) = 1
iff
[[have-always]]c,<wc,tc>(li. [in wi at ti, sc lives at [[here]]c,i]) = 1
(Exercise: Check each step in (20) and annotate it with the rule(s) applied.) Now we can't continue further without specific assumptions about here and have-always. As for here, we are entertaining two lexical entries, the indexical one in (2) and the non-indexical one in (3). Each of these will yield a potentially different prediction:
(21) Prediction of indexical
analysis:
The utterance of (16) in c is true
iff
[[have-always]]c,<wc,tc>(li. [in wi at ti, sc
lives where sc
is in wc at
tc]) = 1
(22) Prediction of
non-indexical analysis:
The utterance of (16) in c is true
iff
[[have-always]]c,<wc,tc>(li. [in wi at ti, sc
lives where sc
is in wi at ti]) = 1
What each of these says will depend on our lexical entry for have-always, which in principle now we can make up as it suits us. We will argue two things: First, we show that it is easy to write an entry for have-always which turns (21) into the intuitively correct prediction. Second, we argue that it is impossible to write an entry for have-always which would make (22) the intuitively correct prediction. Having established those two things, then, we will conclude that (21) is supported over (22), and accordingly that the indexical analysis of here is supported over the non-indexical one.
The successful entry for have-always that will make (21) correct is straightforward[22]:
(23) [[have-always]]c,i = lp<s,t>."t < ti: p(wi,t) = 1
Plugging (23) into (21), we obtain:
(24) Prediction of indexical
analysis:
The utterance of (16) in c is true
iff
"t < tc: in wc at t, sc lives where sc is in wc at tc
(Exercise: Derive (24) from (21) and (23).) This is the intuitively correct reading. If John uttered (16) in Somerville today, for instance, then (24) predicts that he spoke falsely unless he lived in Somerville at all times before today.
So we have seen that there is some entry for have-always in conjunction with which the indexical analysis of here works right. To complete our argument, though, we must now also show that there is no plausible entry for have-always that would combine into an equally successful package with the non-indexical entry of here. Naturally, a general negative claim like this is harder to establish, and we will not give a real proof here, just an informal plausibility argument.
According to (22), you can determine the truth-value of (16) in c on the basis of the proposition that's the argument of [[have-always]]c,<wc,tc>, namely the proposition li.[in wi at ti, sc lives where sc is in wi at ti] Ð let's call it p. p in effect tells you, for any possible world-time pair, whether or not sc's residence coincides with sc's location (in other words, whether sc is at home). But it tells you nothing about whether sc ever moved. For however many world-time pairs I tell you the truth-value of p, you won't know anything about in which worlds and at which times sc changed residence. Intuitively, however, that information is crucial for the truth or falsity of (16). So it appears that the world-time pairs at which (16) is intuitively true cannot be identified on the basis of p, as (22) implies they can be.
So if indeed we can't come up with an entry for have-always that succeeds in conjunction with the non-indexical analysis of here, then we have another roundabout argument for the indexical analysis. The indexical analysis made it possible for us to capture the fact that, even though here in (16) is in the scope of have-always, the structure has the same meaning as if here had been scoped out. In other words, with the indexical entry of here and our entry (23) for have-always, we predict that (16) is equivalent to (25).
(25)
Exercise: Prove this equivalence, i.e., show that (16) and (25) have the same character.
The fact that here acts just as if it had wide scope w.r.t. the temporal operator always is part of a broader generalization that we suggested in our discussion in section 2, viz. that here and other indexicals never show detectable narrow scope w.r.t. anything. More precisely: there is no case where a structure in which here is in the scope of some item has a different meaning then a minimally differing structure in which here has been moved out of that item's scope. Here is a schematic display of such a minimal pair of structures:
(26) (a)
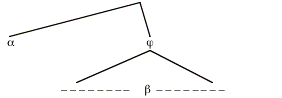
(b)
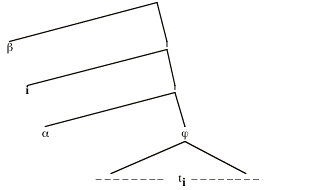
b stands for an indexical (say here), and a is some arbitrary expression (such as the operator have-always). In structure (a), b is in the scope of a; structure (b) differs minimally in that b has been moved above a, leaving the trace ti. The generalization is that, if b is an indexical, then (26a) and (26b) will be semantically equivalent (have the same character), no matter what a is and what's in j.
Can we prove that this generalization follows from the assumption that b is an indexical? Not quite in full generality, but we can if we restrict the claim to indexicals whose extensions are of type e and which don't contain any variables free in them.[23] Still, then, the claim is very general, because of the numerous options for the semantic types of a and j. Let us single out one special case here, namely the case of a being a modal or temporal operator. This means that a has an extension of type <st,t>), and j an extension of type t.
Exercise: Show that under the assumptions just specified (i.e., b is an indexical with an extension of type e, and a has an extension of type <st,t>), (26a) and (26b) must be equivalent.
In sum, we have seen in this section that when a word is not an indexical, then its scope w.r.t. a temporal or modal operator can affect truth-conditions. When it's an indexical, on the other hand, wide and narrow scope w.r.t. a given operator always yield identical truth-conditions. People therefore say that indexicals are "scope-less". This does not mean that the notion of "scope" is not defined for them. Just as with any other expression, the scope of an indexical is its sister-constituent at LF. What is meant by "scopelessness" is just that it makes no interpretive difference whether or not an indexical is moved out of the scope of a modal/temporal operator.
4. Scopelessness (non-shiftability): Indexicals (words whose extension depends only on the context, not on the evaluation point) always are interpreted as if they had widest scope with respect to any quantificational elements (such as modal and temporal operators). Their reference never "shifts" in embedded contexts. The reason is that operators always quantify over evaluation points, never over contexts.
Operators like have-always quantify over evaluation times, or -- as it is also put in semanticist's jargon -- they shift the evaluation time. It's the simultaneous existence in English of such evaluation-time shifters and of speech-time relative adverbs like today and now (whose extension depends on the utterance time, no matter how deeply they are embedded) that makes it necessary to include a time-coordinate in the point of evaluation. If there were no operators that shift evaluation time, we could get away with the time determined by the context alone.
This suggests a way to decide what other coordinates we must include in the point of evaluation. As Lewis (1980)[24] points out, this is an empirical issue and depends on what kinds of operators occur in English and other natural languages. It is entirely conceivable in principle, for instance, that English might have contained an operator "putting-myself-in-your-shoes" with a semantics such that "putting-myself-in-your-shoes, I am tired" would have meant that you are tired. In that case, we should have included a speaker-coordinate in the point of evaluation and should have written the entry for I so that its extension is this "evaluation speaker" rather than the speaker of the utterance context. But since there seems to be no such operator, we will not do this.
Shiftability and the principle of Intensional Compositionality
The reasoning just presented presupposes that whatever is shifted by any operator is ipso facto a coordinate of the point of evaluation rather than of the context. Why should we assume this? Concretely, if we were indeed to discover the hypothetical operator "putting-myself-in-your-shoes" with the semantics just indicated, couldn't we just as well leave the entry for I as it is and interpret the operator as follows?
(20) For any context c, any
point of evaluation i, any proposition-character k:[25]
[[putting-myself-in-your-shoes]](c)(i)(k) = 1
iff k(c')(i) = 1 for that c' which differs from c only in
that sc' =
the individual whom sc
addresses in wc at
tc.
It may not be apparent at first sight, but (20) is problematic. A minor objection is that, if we admitted such lexical entries, we would need a new clause in the Functional Application rule. This in itself needn't stop us, because such a clause can easily be written. (Exercise: Write it.) In addition, however, there is a problem with the definition of c'. As it is defined in (20), c' will not (except by accident) pick out a context. For recall that not any random triple of a world, time, and individual is a context; only those triples are where the individual happens to perform an utterance at that world and time. So since characters are defined to be functions from contexts to intensions, k(c') will usually not be defined, and (20) thus doesn't really say what we intended it to. We could fix this technical problem by redefining characters as functions whose domain is a larger class of world-time-individual-triples than just the contexts. But in doing so, we would substantially alter the theory, returning, in effect, to a version of the previous expanded-index approach which made no principled distinction between contexts and points of evaluation.
An operator like the one defined in (20) would allow the intension of the sentence containing it at a given context c to depend not just on the intension of the embedded sentence at c, but rather on its whole character, viz. on its intensions at contexts other than c. Such an operator is what Kaplan (1977) called a "monster", and he proposed not to admit such items in one's semantic theory.[26] One way of adopting this constraint is by holding on to the Principle of Intensional Compositionality, even as one adopts a semantic framework in which semantic values are generally characters rather than intensions.[27]
(21) Principle of
Intensional Compositionality:
The intension of each phrase at a given context is determined by the intensions
of its immediate constituents at that same context.
Some quotes to think about
Kaplan[28], p. 502:
"Thus if I say, today,
I was insulted yesterday
and you utter the same words tomorrow, what is said is different. If what we say differs in truth-value, that is enough to show that we say different things. But even if the truth-values were the same, it is clear that there are possible circumstances in which what I said would be true but what you said would be false. Thus we say different things.
Let us call this first kind of meaning - what is said - content."
Lewis (1980)[29], p 97:
"Consider some further examples. (1) I say 'I am hungry.'. You simultaneously say to me 'You are hungry.'. What is said is the same. (2) I say 'I am hungry.'. You simultaneously say 'I am hungry.'. What is said is not the same. Perhaps what I said is true but what you said isn't. (3) I say on 6 June 1977 'Today is Monday.'. You say on 7 June 1977 'Yesterday was Monday.'. What is said is the same. (4) Same for me, but you say on 7 June 1977 ' Today is Tuesday.'. What is said is the same. (5) I say on 6 June 1977 'It is Monday.'. I might have said, in the very same context, '6 June 1977 is Monday.' or perhaps 'Today is Monday.'. What is said is not the same. What I did say is false on six days out of every seven, whereas the two things I might have said are never false.
I put it to you that not one of these examples carries conviction. In every case, the proper naive response is that in some sense what is said is the same for both sentence-context pairs, whereas in another - equally legitimate - sense, what is said is not the same. Unless we give it some special technical meaning, the locution 'what is said' is very far from univocal. It can mean the propositional content, in Stalnaker's sense (horizontal or diagonal). It can mean the exact words. I suspect it can mean almost anything in between. [...]
Kaplan's readers learn to focus on the sense of 'what is said' that he has in mind, ignoring the fact that the same words can be used to make different distinctions. For the time being, the words mark a definite distinction. But why mark that distinction rather than others that we could equally well attend to? It is not a special advantage of [Kaplan's choice of] semantic values that they can easily be used to explicate those distinctions that they can easily be used to explicate."
Kaplan, pp. 514 - 15:
"Suppose I point at Paul and say,
(1) He now lives in Princeton, New Jersey.
Call what I said -- i.e., the content of my utterance, the proposition expressed -- 'Pat'. Is Pat true or false? True! Suppose that unbeknownst to me, Paul had moved to Santa Monica last week. Would Pat have then been true or false? False! Now, the tricky case: Suppose that Paul and Charles had each disguised themselves as the other and had switched places. If that had happened, and I had uttered as I did, then the proposition I would have expressed would have been false. But in that possible context the proposition I would have expressed is not Pat. That is easy to see because the proposition I would have expressed, had I pointed to Charles instead of Paul -- call this proposition 'Mike' -- not only would have been false but actually is false. Pat, I would claim, would still be true in the circumstances of the envisaged possible context provided that Paul -- in whatever costume he appeared -- were still residing in Princeton."
Kaplan, pp. 519:
"I have carefully avoided arguing for the direct reference theory by using modal or subjunctive sentences for fear the Fregean would claim that the peculiarity of demonstratives is not that they are rigid designators but that they always take primary scope. If I had argued only on the basis of our intuitions as to the truth-value of
(2) If Charles and Paul had changed chairs, then he [pointing at Paul] would not now be living in Princeton
such a scope interpretation could be claimed. But I didn't."
6. Covertly indexical expressions
6.1. Quotes from Kripke[30]
"... though Jonah did exist, no one did the things commonly related to him." (p. 67)
"Hitler might have spent all his days in quiet in Linz." (p. 75)
"The mere discovery that there was indeed a detective with exploits like those of Sherlock Holmes would not show that Conan Doyle was writing about this man." (p. 157)
"Gold apparently has the atomic number 79. Is it a necessary or a contingent fact about gold that it has the atomic number 79? Certainly we could find out that we were mistaken. ... Certainly we didn't know it from time immemorial. So in that sense, gold could turn out not to have atomic number 79. ... Given that gold does have the atomic number 79, could something be gold without having the atomic number 79? ... Suppose we ... find some other metal yellow metal ... with all the properties by which we originally identified gold, and many of the additional ones that we have discovered later. ... we wouldn't say that this substance is gold. ... In any counterfactual situation where the same geographical areas [where we in fact find gold] were filled with such a substance, they would not have been filled with gold." (pp. 124 - 25)
"Cats are in fact animals. ... Consider the counterfactual situation in which in place of these creatures -- these animals -- we have in fact little demons which when they approached us brought bad luck indeed. ... It seems to me that these demons would not be cats. They would be demons in a cat-like form. We could have discovered that the actual cats we have are demons. Once we have discovered, however, that they are not, it is part of their very nature that, when we describe a counterfactual world in which there were such demons around, we must say that the demons would not be cats. Although we could say that cats might turn out to be demons,... given that cats are in fact animals, any cat-like being which is not an animal, in the actual world or a counterfactual one, is not a cat." (pp. 125- 26)
"..., the mere discovery of animals with the properties attributed to unicorns in the myth would by no means show that these were the animals the myth was about: perhaps the myth was spun out of whole cloth, and the fact that animals with the same appearance actually existed was mere coincidence. In that case, we cannot say that the unicorns of the myth really existed; we must also establish a historical connection that shows that the myth is about these animals." (p. 157)
6.2. Characters for proper names
The proper name Frege, as used for instance by me in this class, refers to a certain person. This person is its extension. In our semantic theory, the extension of an expression is determined by (i) its character, (ii) the utterance context, and (iii) the point of evaluation. What is the contribution that each of these three determinants makes to the fact that my use of Frege has this person rather than some other person as its extension?
Kripke informally considers and refutes a number of possible answers to this question, among them the following.[31]
(1) [[Frege]]c,i = the unique individual called "Frege" by his contemporaries in wi.
(2) [[Frege]]c,i = the unique German philosopher who wrote "Begriffsschrift" and "†ber Sinn und Bedeutung" in wi.
He points out, for instance, that lexical entries like (1) and (2) would falsely predict (3) and (4) respectively to be contradictions.
(3) Frege was not called "Frege" by his contemporaries.
(4) Frege did not write "Begriffsschrift".
Intuitively, these sentences are probably false but by no means contradictory. (1) and (2) also predict wrong truth conditions for counterfactual conditionals like (5) and (6).
(5) If Frege's mother had left him as a new-born baby on the doorstep of the local parish, he would not have been called "Frege".
(6) If Frege had died as a teenager, he would not have written "Begriffsschrift."
To see concretely what goes wrong, let's apply the following ad hoc semantics for counterfactual conditionals:[32]
(7) Abbreviation: Let i be an index, w a possible world. Then iw is that index whose world-coordinate is w and which agrees with i in all other coordinates.
(8) Definition:
€ is a function from pairs of an
index and a proposition to indices, defined as follows:
For any index i, proposition p: €(i,p) = iw, where
w is the unique world which fulfills the following two conditions:
(i) p(iw) = 1, and
(ii) w
resembles wi more
than any other world w' such that p(iw')
= 1.
(9) [[if f, would y]]c,i = [[y]]c,i', where i' = €(i,[[f]]¢c).
Let us apply this semantics to the conditional in (6), assuming the LF in (10) and the lexical entry for Frege in (2).
(10)
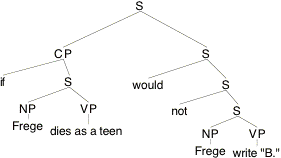
Disregarding temporal matters and identifying indices simply with their world-coordinates, we derive (for any arbitary c, i):
(11) [[(10)]]c,i = 1 iff [[Frege write "B."]]¢c(€(wi, [[Frege dies as a teen]]¢c) = 0.
To determine €(wi, [[Frege dies as a teen]]¢c), w have to look at the set of worlds {w': [[Frege dies as a teen]]¢c(w') = 1} and find in this set the world most similar to wi. But given entry (2), this is the set of w' such that the German philosopher who wrote "Begriffsschrift" and "†ber Sinn und Bedeutung" in w' (!) died as a teen in w'. Whichever element w' we pick from this set, it will not satisfy the condition that [[Frege write "B."]]c, w' = 0. So (11) implies that (10) is false for all w. This, of course, violates the intuition that (10) is true in the actual world.
Similar comments apply to example (5) and entry (1). (Exercise: Show that entry (1) in conjunction with (9) predicts counterintuitive truth conditions for (5).) In each case, one might try to rescue the proposed entry by stipulating somehow that proper names always move at LF to a position where they have widest scope. But this move is unsatisfactory, for the same reasons that it was not a satisfactory solution to the analogous problem with indexicals like here or yesterday (see above).
A more promising solution is to adopt variants of (1) and (2) which make the name Frege directly referential and context-dependent:
(1') [[Frege]]c,i = the unique individual called "Frege" by his contemporaries in wc.
(2') [[Frege]]c,i = the unique German philosopher who wrote "Begriffsschrift" and "†ber Sinn und Bedeutung" in wc.
With these two entries, we make the correct predictions about which propositions the sentences (5) and (6) express when they are uttered in the actual world. (Exercise: Show this for one of the two examples.) And Kripke would agree that they are on the right track insofar as they acknowledge the direct referentiality[33] of proper names. But he still wouldn't accept either of them as correct:
To see what is still wrong, consider examples (3) and (4) once more. In contrast with the previous entries (1) and (2), (1') and (2') predict that utterances of these sentences express contingent propositions. For instance, if (3) is uttered in the actual world, then, according to entry (1'), it expresses a proposition which is false in the actual world but true in certain non-actual worlds (for instance those where Frege's mother abandons him as an infant, and those who find and raise him give him their own family name). Still, (1') predicts that every possible utterance of (3) is false, i.e., expresses a proposition which is false in the world of utterance. If this is so, however, any speaker who has the name Frege in his vocabulary and assigns it the same meaning as we do should know on the basis of his semantic competence alone that no utterance of (3) is ever true. This is wrong. To the extent that we know that Frege's contemporaries called him "Frege", this is factual knowledge (knowledge of a historical fact about Frege) and not linguistic knowledge. Analogous comments apply to example (4) and entry (2'). Those of us who know that Frege wrote "Begriffsschrift" know a biographical fact about him, but others can use the name just as competently and felicitously without this knowledge. And if it were discovered next year (unlikely but certainly possible) that Frege did not after all write the "Begriffsschrift" but plagiarized it from a since forgotten contemporary, this would be a discovery about the man Frege and not about the semantics of the name Frege.
What, then, is the character of a proper name? Kripke explicitly declines to make a constructive proposal, and for good reasons. The upshot of his discussion is that the task of specifying exactly how the reference of a name depends on the context in which it is uttered is similar to the analogous task for a demonstrative or 3rd person deictic pronoun. In that case, we said that the referent was the individual "demonstrated" by sc in wc at tc, but we didn't provide a real definition of what it is to demonstrate something. We mentioned some paradigmatic cases of demonstration (pointing, exploiting perceptual salience) and left it at that, without trying to give an exhaustive characterization. We will proceed similarly in the case of proper names. This time, our catch-all artificial locution is that a particular use of a name is "appropriately connected" to a certain individual. When asked what we mean by "appropriately connected", we describe some paradigmatic instances. For example, if a person x is baptized with the name a, then introduced as a by his parents to other people, from whom yet other people pick up the name and pass it on to others, who pass it on further until it ultimately gets to sc, the subsequent uses of a by sc count as appropriately connected to x. More complicated scenarios are possible, some of them alluded to by Kripke and others yet discussed in subsequent literature.[34] We are not denying that it is interesting and perhaps important to attempt a more complete and precise characterization of this concept, but we assume that this a job for someone other than the formal semanticist. So we leave it at this superficial sketch and propose the following lexical entry for the name Frege:
(12) [[Frege]]c,i = the unique individual to whom sc's use of the expression Frege in wc at tc is appropriately connected; undefined if there is no unique such individual.
Semantic competence regarding a proper name is thus is a very minimal ability. The lexical entries of all proper names conform to the same schema as (12), so as soon as I realize that a given expression is a proper name, I can predict its lexical entry. I needn't know anything that would help me identify its bearer -- probably not even whether it's a person, and certainly not whether it is a philosopher, what it has written, or what its contemporaries called it.
6.3. Characters for common nouns
Putnam (in various papers[35]) and Kripke (op. cit.) have shown that the semantics of a lot of the vocabulary of natural languages is rather like that of proper names. Just as it is not determined by the meaning of the proper name Frege that its bearer should have been a German philosopher, written the "Begriffsschrift", or anything of this sort, it is not determined by the meaning of the common noun cat that cats should be animals, meow, or have an instinctive urge to lick themselves, and it is not determined by the meaning of the common noun copper that copper should be a metal, be reddish, or have the atomic number 29. All one needs to know in order to understand one of these predicates is that it applies to a given object only if that object is of the same kind as other objects to which the predicate is typically applied by members of one's linguistic community. Once again, we avail ourselves of a term of art and say that the use of a common noun in a given utterance is "appropriately connected" to a kind. What this means can be explicated in more or less detail, and we refer for such explications to the pertinent philosophical literature. Our lexical entries read as follows.
(13) [[copper]]c,i = lx. x in wi at ti is stuff of a kind to which sc's use of the expression copper in wc at tc is appropriately connected.
(14) [[cat]]c,i = lx. x in wi at ti is a thing of a kind to which sc's use of the expression cat in wc at tc is appropriately connected.
Once again, this analysis implies that it takes very little to master the semantics of one of these common nouns. If (13) and (14) are correct, you need to know whether the expression in question is a count noun or a mass noun, but once you know this much, you can predict its lexical entry.
In the case of proper names, we don't have much of a pretheoretical notion of what their "meaning" is. Names don't really count as part of the vocabulary of any particular language; we don't worry much about them when we memorize the vocabulary of a foreign language, and we usually (though not always) leave them unchanged when we translate. It is otherwise with common nouns. If a German learning English doesn't know that coppertranslates as Kupfer and cat as Katze, we would say that she has incomplete knowledge of the English language. But the semantic analysis for common nouns that we have just proposed doesn't seem to predict this intuitive judgment. If the lexical entries in (13) and (14) are all there is to be known about the meanings of these words in English, it should be rather easy to get an A in the language exam.
Our proposal has further counterintuitive consequences of this type.[36] For instance, it seems to imply that any two homophonous mass nouns in two different languages have identical meanings. For instance, English and German both have a mass noun that is spelled and pronounced "mist". In English, it means something like 'fog', and in German it means 'dung'. But if a lexical entry analogous to (13) is right for the English noun mist, it is presumably just as correct for the German homophone. The two then have identical lexical entries, which ought to mean that they have identical meanings.
For another weird prediction, imagine a hypothetical language L which is just like English, except that the noun pronounced 'elm' there applies to beeches, and the noun pronounced 'beech' to elms. If (13) and (14) are correct, then the lexical entries for elm in English and L will presumably be identical, and so will the lexical entries for beech in the two languages. So each phonological shape is predicted to have the same meaning in both languages. In fact, English and L are predicted to be one and the same language, because their grammars and lexica are the same. But our intuitive judgment is that they are different languages. And if an interpreter from English to L translated 'elm' as 'elm' and 'beech' as 'beech', we would say that he translated wrong. He should have translated 'elm' as 'beech' and 'beech' as 'elm'.
There are two different morals that one can draw from these observations. One moral is this: If our goal is to explicate pretheoretical notions of sameness of meaning, sameness of languages, correct translation, etcetera, then our present proposal is grossly inadequate.[37] But another moral is that these pretheoretical notions may not, after all, be particularly interesting from the point of view of a theory of linguistic competence. It is arguable that entries like (13) and (14), however little justice they may do to our pretheoretical semantic concepts, nevertheless represent quite adequately what it takes for a speaker to know the bare linguistic meaning of a common noun. Whatever else she may know, and be expected to know, about copper, cats, mist, elms, or beeches is just encyclopedic knowledge. It follows that a competent translator, for instance, needs a lot more than linguistic competence in the two languages. But then that's really no news to anybody in the translating profession.
7. Meaning and cognitive value: the simple picture[38]
Semantic competence:
What a person knows when s/he knows what a word, phrase, or sentence means in his/her language is its character.
How semantic competence is used in communication:
A speaker s believes a certain proposition p and wants to communicate this to a hearer h. To do so, s must utter a sentence f that expresses p in the context c which s and h are in. s's knowledge of the characters of all sentences in her language enables her to choose a f that has this property, i.e. [[f]](c) = p. h in turn, upon hearing f, uses his semantic competence to recover the character [[f]], applies that to the context c, and thus finds the proposition p. So he comes to know that s presents herself as believing p, and as wanting him to believe it too. h then may or may not come to hold the belief that p, depending on how consistent it is with his other beliefs and how much he trusts s.
There is one rather obvious reason why it can't be quite that simple: neither s nor h could possibly know exactly which context they are in. Recall that contexts are triples of a world, time, and speaker. So knowing exactly which context one is in would require omniscience regarding the facts which obtain in the context-world. Assuming that s and h indeed happen to be in c, neither of them could possibly know this. Evidently, communication is somehow possible without such omniscience.
Fortunately, the characters of natural language sentences (especially those short enough for a human to process) typically do not make very fine discriminations in the vast set of all possible contexts. They lump together large subsets thereof by mapping them to the same value. For instance, a sentence which contains no other context-dependent words than I has a character that assigns the same proposition to any two contexts which have the same third coordinate. For s and h to be sure that s's utterance of f indeed expresses p rather than some other proposition, it therefore typically suffices that they know themselves to be in one of the contexts in a certain very large set. They needn't know which of the numerous elements of this set they are in. They may be ignorant about any properties of the context world at the context time except those few that really play a role in determining the value [[f]] yields.
Actually (as Stalnaker discusses), it's not really knowledge that is called for, but shared presumptions. s may successfully use f to communicate the proposition p to h, even though the context which the two of them in fact are in is not one which [[f]] maps to p. What matters are not the actual facts, or what either of them knows about them, or even what either of them privately believes them to be. What matters is what each takes them to be and assumes the other to take them to be as well. We call this body of shared presumptions the common ground. It can be characterized as a set of possible contexts, namely that set which s and h might be in for all they presuppose[39] in c. This is Stalnaker's "context set".[40]
Let us henceforth use capital letters C, C', ... for sets of contexts (i.e., certain kinds of subsets of W«T«D) and adopt the following abbreviatory convention:
(1) [[f]](C)
:= that proposition p such that [[f]](c)
= p for all c ë C;
undefined if there is no such p.
So here is the picture that has emerged so far (revised from the first paragraph above): A speaker s believes a certain proposition p and wants to communicate this to a hearer h. To do so, s must utter a sentence f that expresses p in all the contexts in Cc, the common ground which she and h share in c.[41] s's knowledge of the characters of all sentences in her language enables her to choose a f that has this property, i.e. [[f]](Cc) = p. h in turn, upon hearing f, uses his semantic competence to recover the character [[f]], applies that to the common ground Cc, and thus finds the proposition p. So he comes to know that s presents herself as believing p, and as wanting him to believe it too. h then may or may not come to hold the belief that p, depending on how consistent it is with his other beliefs and how much he trusts s.
Unfortunately, there are a few reasons why this simple picture can't be quite right -- or at least, why it can't be right in conjunction with the assumptions to which we have already committed ourselves in this course, in particular in the chapter on indexicality.
8. Belief content and belief change
Our picture of communication rests on the assumption that it is propositions, i.e. char. functions of subsets tof W«T, that people believe and communicate to each other in conversation. David Lewis has shown this assumption to be incorrect.[42]
[.... summary of Lewis's arguments in Lewis (1979) ....]
According to Lewis, the content of someone's beliefs (at a given time) is a property, which in his ontological framework means: a set of time-slices of possible individuals. Intuitively, the content of what John believes (in the actual world at the present moment) is the set of all those elements of D which might be him for all he believes. (Lewis (1986) also calls this the set of John's doxastic alternatives.) We will here take such a property to be a set of triples in W«T«D. If the third member of such a triple is a momentary stage of an individual which exists in just one world, then the first two members are uniquely determined by it (as the world which it inhabits and the time it occupies) and so are redundant. But this redundancy is harmless, and we stick to triples to facilitate comparison with theories based on different ontological frameworks.[43] Accepting Lewis's point about belief content, we may continue to say that it is "propositions" that people believe, provided that we say that propositions are functions from indices to truth-values and indices are triples in W«T«D.
Is this reinterpretation of the notion "proposition" all that it takes to make our simple picture of communication consistent with Lewis's theory of belief-content? It'll suffice, presumably, when we stick to examples of what Lewis calls "propositional" belief, where the 3rd coordinate of the triples is idle. But let us check whether it also works for those examples of communication in which the belief that the speaker wants to communicate is one of those which have, speaking with Lewis, an essentially "non-propositional" content.
Suppose s is the famous man whose pants have caught fire, and h is with him at the time when he catches sight of his reflection in the store window. At the moment when s suddenly acquires the belief that his own pants are on fire (=: p)[44], he may want to communicate this belief to h. What words will he use? If he speaks English, he will say something like My pants are on fire (=: f). Intuitively, this sentence is perfectly suited to communicate the belief under consideration in the described situation. So if our simple picture is right, it should be the case that
(i) [[f]](Cc) = p, where Cc is the common ground of this utterance context,
and furthermore that
(ii) h, if he understands and trusts s, comes to believe p as well.
Let's defer a closer look at (i) until later. As regards prediction (ii), it is evidently wrong. To see this, we only need to look at what p is. p is supposed to be the content of the belief that s acquires at the moment when he recognizes that his own pants are on fire, and that is the following function:
(2) For any <w,t,x> ë W«T«D: p(w,t,x) = 1 iff x's pants in w at t are on fire in w at t.
If p were what h comes to believe when he hears, understands, and accepts s's assertion of f, he would wind up believing that his own pants are on fire. This he won't, of course (or, if he does, we will diagnose a drastic misunderstanding rather than a case of successful communication).
The flaw that this example reveals in our simple picture of communication seems to be that we haven't told the right story of what happens on the receiving end. The hearer's job, apparently, is a bit more complicated than we have made it out to be. First, he must indeed determine what property it was that the speaker in his utterance ascibed to himself. But then he can't just go ahead and ascribe that same property to himself. Rather he has to ascribe it to the speaker; which means that, to himself, he must ascribe an appropriately different property. In our example, for instance, h should wind up ascribing p to s, which -- following Lewis's definition (1979, p. 153) -- amounts to ascribing to himself a certain different proposition prc which is determined by p as follows:
(3) For
any proposition p, any acquaintance relation r, and any <w,t,x> ë W«T«D:
<w,t,x> is in the domain of pr only if it is in the domain of r;
where defined, pr(w,
t, x) = 1 iff p(w, t, r(w,t,x) ) = 1.
r here stands for a relation of acquaintance, for instance the relation that h bears to s (in the world and at the time of our little drama) by virtue of his looking at and listening to him. Technically, we treat r as an individual concept (a function that assigns individuals to world-time-individual triples). In the case at hand, let's say it is that function rc which assigns to each <w,t,x> the unique individual whom x is looking at and listening to in w at t -- unless there is no unique such individual, in which case <w,t,x> is not in the function's domain.
As defined in (3), prc depends not only on p but also on rc, so it is not fully determined by p alone. How is rc fixed in a given instance of communication? Let's assume it is the[45] relation by which the hearer in the context in question identifies (represents to himself) the speaker, whatever relation this may happen to be. Since a context c is fully determinate regarding all facts of the context-world at the context-time, it also determines this acquaintance relation, so we can refer to it by writing "rc".
This, then, is the third version of our picture of communication: A speaker s believes a certain proposition p (now taken to be a function from triples) and wants to communicate this to a hearer h. To do so, s must utter a sentence f that expresses p in all the contexts in Cc, the common ground which she and h share in c. s's knowledge of the characters of all sentences in her language enables her to choose a f that has this property, i.e. [[f]](Cc) = p. h in turn, upon hearing f, uses his semantic competence to recover the character [[f]], applies that to the common ground Cc, and thus finds the proposition p. So he comes to know that s presents herself as believing p, and as wanting him to believe prc, as defined above in terms of p and c. h then may or may not come to hold this belief, depending on how consistent it is with his other beliefs and how much he trusts s.
Something to think about:
In the example under consideration, the interlocutors are spatially very close to each other and communication is more or less instantaneous. This, of course, is not always the case. Communication (e.g. by letters) often occurs successfully across long distances in space as well as in time. In such cases, the hearer faces an especially non-trivial job of "translating" the proposition initially believed and expressed by the speaker into a suitably different one for himself to believe. Imagine a concrete example of this kind, determine whether our current assumptions and definitions handle it appropriately, and specify any needed amendments.
Before we can take our burning-pants example to have been treated adequately, we have yet to verify the correctness of our first prediction (= (i)), namely that [[f]](Cc) = p. For this we need to refer to our semantics for English, especially the lexical entry for the first person pronoun. This, of course, is (4).
(4) For any context c, any point of evaluation i: [[I]](c)(i) = sc.
(When we first wrote this, our indices were world-time pairs, whereas now we have redefined them as triples; so "i" now stands for elements of W«T«D.) Applying the standard composition rules and a Fregean semantics of the definite article[46], our sentence gets the following character.
(5) For any
context c, any point of evaluation <w, t, x>:
[[My pants are on fire]](c)(w,t,x) = 1 iff
the (unique pair of) pants that sc has w at t are on fire in w at t.
What, then, is [[My pants are on fire]](Cc)? Recall that this is not defined in the first place unless [[My pants are on fire]] yields the same value for all c' in Cc. As a whole, [[My pants are on fire]] is clearly not a constant function. But its restriction to Cc may still be constant, provided that all elements of Cc have the same speaker-coordinate. Intuitively, this sort of means that s and h agree in c on who it is that's speaking. Below we will take a closer look at what this means exactly, and we will see that it is not such an innocuous assumption after all. But for now, let's assume it is indeed fulfilled. So there is a certain individual, call it sCc, such that sc' = sCc for all c' ë Cc.[47] The proposition [[My pants are on fire]](Cc) is then determined by (5) as follows:
(6) For any
point of evaluation <w, t, x>:
[[My pants are on fire]](Cc)(w,t,x) = 1
iff
sCc's pants in w at
t are on fire in w at t.
Now we can ask our crucial question: Is this the same proposition as p, the content of the belief s wants to communicate, as defined in (2) above? The answer is: No, it isn't. The domain of p surely contains at least some triples <w,t,x> such that x sCc, x's pants are on fire in w at t , and sCc's pants are not. For any such triple <w,t,x>, we have p(w,t,x) = 1 but [[My pants are on fire]](Cc)(w,t,x) = 0. So the two propositions are not the same.
This seems at first to be a problem for our current picture of communication. But one can argue that it isn't really. The argument rests on the observation that p and [[My pants are on fire]](Cc), though undeniably distinct overall, coincide in a certain important part of their common domain, namely within the common ground. How so? Well, let's see what happens when we feed either proposition an argument that's an element of Cc. Suppose <w,t,x> is an arbirtary member of Cc. Then, by assumption, x = sCc. But this implies that sCc's pants are on fire in w at t iff x's pants are on fire in w at t, and therefore p(w,t,x) = [[My pants are on fire]](Cc)(w,t,x). Since <w,t,x> was an arbitrary element of Cc, we infer that p restricted to Cc is the same function as [[My pants are on fire]](Cc) restricted to Cc.[48]
How does this restricted identity help to rescue our picture of communication? Why is the divergence of the two propositions outside of the common ground somehow harmless? There is a pretty straightforward answer to this question for the special case where the conversation is sincere and serious. In this case, each interlocutor's beliefs are consistent with the common ground: they don't presuppose anything that they don't really believe. Technically, this means that s's set of doxastic alternatives is a subset of the common ground (Doxs ê Cc), and analogously for h (Doxh ê [Cc]rc). When h now accepts some new proposition p into his beliefs, this amounts to intersecting Doxh with prc. The outcome of this intersection evidently depends only on the restriction of prc to Doxh; it is not affected by the behavior of p outside of Doxs, and -- since Doxs ê Cc -- a fortiori not by its behavior outside Cc. So we can see why it is sufficient for communicative success if h can recover from s's utterance a partial proposition with domain Cc.
Things are not so straightforward when the common ground includes presuppositions that h doesn't really believe. In this case, if he recovers from s's assertion only a partial proposition defined within Cc, this may underdetermine the adjustment that he should make to his real beliefs when he believes what s said. But perhaps that's as it should be: It makes sense intuitively that when a conversation is conducted under presuppositions that are more or less far removed from one's real beliefs, it's not always clear what real information to draw from it. [I should illustrate this point with a concrete example.]
What we conclude from the discussion of our burning-pants example, then, is that another refinement of our picture of communication is called for, but not a drastic one. Here is the fourth version, with which we conclude this section: A speaker s believes a certain proposition p (a function from triples in W«T«D) and wants to communicate this to a hearer h. To do so, s must utter a sentence f which in all the contexts in Cc (the common ground which she and h share in c) expresses a proposition p' such that pŽCc = p'ŽCc. s's knowledge of the characters of all sentences in her language enables her to choose a f that has this property, i.e. [[f]](Cc)ŽCc = pŽCc. h in turn, upon hearing f, uses his semantic competence to recover the character [[f]], applies that to the common ground Cc, and thus finds the proposition pŽCc. So he comes to know that s presents herself as believing[49] pŽCc, and as wanting him to believe [pŽCc]rc, as defined in (3) above in terms of pŽCc and c. h then may or may not come to hold this belief, depending on how consistent it is with his other beliefs and how much he trusts s.
9. Communication by diagonalization
Stalnaker (1978) discusses a number of examples that cannot be adequately dealt with in the picture of communication we have arrived at so far. The first of the examples that we will use to replicate his point and illustrate his solution is a variant of the burning-pants scenario we have considered so far. It involves the same two people s and h, and once again the story starts with s and h walking along together and catching sight of a man with burning pants reflected in a store window. But in this story, s doesn't notice that it's he himself. So what he believes is not p, but the following q, and it is this belief-content which he seeks to communicate this time.
(7) For any <w,t,x>: q(w,t,x) = 1 iff the pants of the individual whom x is demonstrating in w at t are on fire in w at t.
The sentence he chooses to utter for this purpose is not f (My pants are on fire), of course, but rather His pants are on fire (=: y).
What is the belief-content for h at the successful end of this communication event? We expect it to be the following:
(8) For any
<w,t,x> in Cc
and in the domain of rc:
[qŽCc]rc(w,t,x) = 1 iff the pants of
the individual whom rc(w,t,x)
is demonstrating in w at t are on fire in w at t.
If h is to arrive at this, the character [[y]] ought to be such that [[y]](Cc)ŽCc = qŽCc. Let us see if this is the case.
We assume the standard directly
referential semantics for the demonstrative 3rd person pronoun he, as in the following lexical entry:
(9) [[he]](c)(i) = the unique (male) individual whom sc demonstrates in wc at tc
(undefined for c where there is none).
Let's abbreviate "the unique (male) individual whom sc demonstrates in wc at tc" as "demonstratumc". The character of y thus comes out as follows:
(10) For any c in the domain
of [[he]], any <w,t,x>:
[[his pants are on fire]](c)(w,t,x) = 1
iff the pants in w at t of
demonstratumc are
on fire in w at t.
Does our picture of communication predict this character to be suitable for the message s intends to get across?
Our first question in trying to assess this once again must be whether [[y]] is constant across the common ground. Suppose we have an arbitrary pair c', c'' of two contexts that are both in Cc. Under what condition will it be the case that [[y]](c') = [[y]](c'')? (10) determines that it will be the case only if (11) holds.
(11) For any <w,t,x> ë W«T«D:
the pants in w at t of demonstratumc' are on fire in w at t
iff the pants in w at t of
demonstratumc'' are
on fire in w at t.
(11) will hold just in case demonstratumc' = demonstratumc''. This means that [[y]] is constant on Cc only if the same individual is being demonstrated in all contexts in the common ground; in other words, if s and h agree on who it is that's being demonstrated.
Do they? Intuitions are not entirely clear on this. One might argue that they don't at this point; only a little later will they find out who was being demonstrated, namely when s realizes it's him. On the other hand, one might say that they now agree that a certain person different from sCc is being demonstrated, and what they will find out in a few seconds amounts not to a mere increase in information, but rather to a revision of the common ground, in which the earlier presumption about who s was demonstrating is abandoned.
That seems arguable for the particular story at hand. But there are clearly some cases where one must concede that at certain stages of the conversation the interlocutors treat it as an open question who is being demonstrated. This conclusion is most inescapable when we look at utterance situations where the identity of a demonstratum is explicitly under debate, and where the utterance to be analyzed makes a contribution to just this debate. Assertions of identity or non-identity are the most obvious cases in point, and this is why Stalnaker (1978) concentrates on just this type of example.
Our burning-pants example can be sharpened to bring out the problem, if we flesh out the story explicitly so that there is a period where s and h are consciously entertaining the possibility that the speaker may be looking at none other than himself, but have not yet established this as a certainty. This interim period clearly has to be described as one where there is not yet a shared presumption as to who is being demonstrated. Yet, a use of demonstrative he is no less felicitous then.
Imagine, in particular, that our same sentence y (His pants are on fire) is uttered at a time where s and h already suspect that the reflection might be of s himself, but don't yet take it for granted. As we saw from (11) above, [[y]] is not constant across Cc then, but assigns different propositions expressed to different elements of it. To some, for instance, it assigns the proposition that sCc's pants are on fire, but to others one of the propositions that y's pants are on fire for various y sCc.
If this sort of situation arises, Stalnaker argues, the sentence uttered has to be reinterpreted in a certain way by the hearer, so that the new interpretation assigns it a constant character after all. There is a fixed recipe for this reinterpretation, and it consists in applying the so-called diagonalizer to the character originally assigned by the semantics.
The diagonalizer (or diag) is a function from characters to characters, and we define it as follows:[50]
(11) For any character k and context c, diag(k)(c) is a function from contexts to extensions such that, for any context c': diag(k)(c)(c') = k(c')(c').
Notice that a function from contexts to extensions is a partial intension. It is partial because the contexts are a proper subset of all the points of evaluation (the latter are all the triples in W«T«D, the former only those whose 3rd coordinate utters something in the 1st at the 2nd). To illustrate, let's see what we get when we apply diag to the literal character of His pants are on fire, as defined in (10) above.
(12) For any contexts c and
c':
diag([[his pants are on fire]])(c)(c') = 1
iff [[his pants are
on fire]](c')(c')
= 1
iff the pants of demonstratumc' are on fire in wc' at tc'.
diag([[his pants are on fire]]) is clearly a constant function, not just within Cc but on its entire domain. (Notice that the last line of (12) contains no reference to c!) Its value for all arguments is a partial proposition, whose restriction to Cc however is total. Here it is:
(13) diag([[his
pants are on fire]])(Cc)ŽCc is that function f with domain Cc
such that, for any <w,t,x> in its domain,
f(w,t,x) = 1 iff the pants in w at t of the individual
whom x demonstrates in w at t are on fire in w at t.
Intuitively, the diagonalized character of His pants are on fire (restricted to the common ground) is thus the same as the literal character of a sentence like: The pants of whoever I am pointing at are on fire (restricted to the common ground). Diagonalization, so to speak, "converts" indexicals into their context-independent analogues.
Exercise:
Diagonalize the characters which the semantics assigns to the following sentences. In each case, give another English sentence, whose character before diagonalization is the same as the result you have obtained.
(i) The meeting starts now.
(ii) I have always lived here.
Stalnaker's idea is that diagonalization applies as a last resort, namely only in those cases where the literal character fails to be constant across the common ground. I want to raise two questions about this, one technical, the other more substantive.
That diagonalization is only a last resort means that it does not apply when it doesn't need to, i.e. when the literal character of the sentence uttered is constant across the common ground to begin with. As it turns out, however, this assumption is empirically vacuous: An alternative theory which claims that every utterance is understood via diagonalization would make exactly the same predictions. This can be shown as follows:
Suppose an utterance of a sentence f in a context c does not require diagonalization. This means that [[f]] is constant on the common ground, i.e., [[f]](c) = [[f]](c') for all c, c'ëCc. I claim that this implies that diag([[f]])(Cc)ŽCc = [[f]](Cc)ŽCc. Proof: Let c be an arbitrary element of Cc. Then diag([[f]])(Cc)ŽCc(c) = diag([[f]])(Cc)(c) = [[f]](c)(c) = [[f]](Cc)(c) = [[f]](Cc)ŽCc(c). (Exercise: Justify each step in this chain of equalities.) Recall now that according to our picture of communication (as last revised on p. 44 - 45), the result of successful communication depends only on the restriction to Cc of the proposition that the sentence uttered expresses in Cc. Since we have just shown that this restricted proposition is the same, whether we take the literal character or the diagonalized one, superfluous diagonalization will never alter the outcome.
We have yet to officially revise our picture of communication so as to provide for diagonalization, at least in the cases where it is required. But instead of writing a disjunctive condition that distinguishes between the "ordinary" cases and those requiring diagonalization, it is simpler and equivalent (as we just saw) to make diagonalization the general rule. So here is the fifth version:
A speaker s believes a certain proposition p (a function from triples in W«T«D) and wants to communicate this to a hearer h. To do so, s must utter a sentence f which in all the contexts in Cc (the common ground which she and h share in c) expresses a proposition p' such that pŽCc = p'ŽCc. s's knowledge of the characters of all sentences in her language enables her to choose a f that has this property, i.e. diag([[f]])(Cc)ŽCc = pŽCc. h in turn, upon hearing f, uses his semantic competence to recover the character Diag([[f]]), applies that to the common ground Cc, and thus finds the proposition pŽCc. So he comes to know that s presents herself as believing pŽCc, and as wanting him to believe [pŽCc]rc, as defined in (3) above in terms of pŽCc and c. h then may or may not come to hold this belief, depending on how consistent it is with his other beliefs and how much he trusts s.
Homework
(a)
In the fairy-tale "The Wolf and the Seven Little Goats," the little goats are home alone when the wolf knocks on the door and says: "Open the door, my dear little goats! I am your mother."
Analyze the wolf's utterance of the sentence I am your mother in terms of our model of communication. Show, in particular, that this is a case where diagonalization is indispensable.
(b)
The following type of example is due to Geoff Nunberg: Before the mother goat goes out, she instructs the little goats not to open the door to a stranger: "If somebody knocks, ask him to show his hoof in the window, and open the door only if you recognize the hoof as mine." But since she doesn't trust them, she decides to put them to the test. She returns and knocks, and the little goats open the door immediately. She chides them and says: "You shouldn't have opened the door. I could have been the wolf. If I had been the wolf, I would have eaten you all by now."
Discuss the last two sentences of the mother goat's utterance. Are they problematic for our current (and Stalnaker's) theory?
The second, more substantive, question I want to raise about Stalnaker's view on the role of diagonalization is this: What exactly does it mean that the interlocutors agree on who it is that's speaking (or that's being addressed, or that's being demonstrated), and in what sense is such agreement a precondition for successful communication?
The pretheoretical notion of agreeing who someone is seems to be vague and highly flexible, just like the related notion of knowing who someone is. Though we typically know the names of people of whom we would say that we know who they are, this is neither a sufficient nor a necessary condition. For instance, if I found a message in my mailbox "Please call back John Smith", I would say "I don't know who John Smith is." On the other hand, I might not know a person's name when I recognize him in the street and say to him: "I know who you are. You are the guy who waited on our table last night." Other typical conditions (e.g., being able to recognize somebody on sight) also turn out to be neither necessary nor sufficient. And clearly, no such conditions are required in order to have a conversation with or about somebody -- regardless of whether that conversation happens to be about questions of identity or about ordinary matters (like directions to the next bathroom).
So from this point of view, too, it is reasonable to say that we always diagonalize when we process an assertion. So the formulation above of the picture of communication is not just technically more elegant that a disjunctive formulation, but intuitively better motivated as well.
This result is strange in light of the arguments by which we initially motivated the separation of context and point of evaluation. If it really always is the diagonal proposition that the listener must recover in order to understand the utterance, what is the role of the proposition literally expressed? Why should concepts like "answer to a question" or "disagreement" be defined in terms of that rather than in terms of the diagonal proposition?
If the diagonalized character is what really determines the result of successful communication, why don't we change our semantics in such a way that it assigns this as the literal meaning in the first place? In other words, why don't we rewrite the lexical entries for indexicals as follows?
(14) (a) [[I]](c)(w,t,x) = x.
(b) [[here]](c)(w,t,x) = the place which x occupies in w
at t.
(c) [[now]](c)(w,t,x) = t.
(d) [[that guy]](c)(w,t,x) =
the
unique male individual whom x demonstrates in w at t;
undefined
of there is no unique such individual.
(e) [[you]](c)(w,t,x) = the individual whom x addresses
in w at t.
etc.
Exercise:
Show that, with the entries in (14), the literal character of examples (i) - (iii) below comes out the same as their diagonalized character under our official entries.
(i) I like you.
(ii) That guy is dead now.
(iii) I don't live here.
Well, we have already seen the reason why lexical entries like those in (14) are a bad idea: They would lead us straight back into inadequate predictions about the truth conditions of utterances of I have always lived here, I didn't have to be here, You didn't use to know what you know now and the like.
Debris:
Kaplan, p.532:
"If you and I both say to ourselves,
(B) "I am getting bored"
have we thought the same thing? We could not have, because what you thought was true while what I thought was false.
What we must do is disentangle two epistemological notions [...]
E. Principle 1 Objects
of thought (Thoughts) = Contents
E. Principle 2 Cognitive significance of a thought = Character"
Kaplan, p. 539 and fn. 64:
"Suppose that yesterday you said, and believed it, "It is a nice day today." What does it mean to say, today, that you have retained that belief? It seems unsatisfactory to just believe the same content under any old character - where is the retention?
The sort of case I have in mind is this. I first think, "His pants are on fire." I later realize, "I am he" and thus come to think "My pants are on fire." Still later, I decide that I was wrong in thinking "I am he" and conclude "His pants were on fire." If, in fact, I am he, have I retained my belief that my pants are on fire simply because I believe the same content, though under a different character?"