







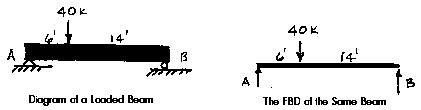
Solution:
The reactions at A and B are replaced by forces at A and B. The force at B must be vertical because its roller support can only react perpendicular to the surface upon which it rests. The line of the 40k load and the reaction at B have no horizontal components so it should be clear that the horizontal component of A must be zero. Therefore, it is not shown. If we assumed a horizontal component at A and showed it on the FBD, we would find through the "sum of the horizontal forces equals zero" that the horizontal component was zero. It would still be a valid FBD. Everything that is needed to solve the FBD is shown.
Now use the FBD and the principles of equilibrium, "sum of the forces must equal zero" and "sum of the moments must equal zero," to solve for the unknown forces.
If we try to solve for the vertical forces, we have two unknowns and only one equation. If we track moments about the line of action of either A or B, we will have a moment equation with only one unknown. For this reason, points A or B are convenient points around which to take the moments.
If we take the moments around point A, Sum MA = 0, we know that the absolute value of the counter-clockwise moments must equal the absolute value of the clockwise moments.
The reaction at point A may now be found either by taking the moments around point B, Sum MB= 0, or by summing the vertical forces, Sum Fy= 0, and using the reaction at B found above.
To check:
Sum Fy = 12k + 28k - 40k = 0