Combined Moment Example Problem

Lecture 5
Example Problem

Calculating a Combined Moment

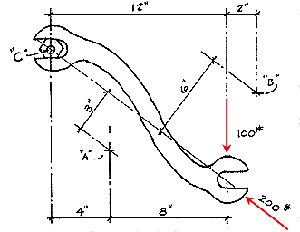
monkey wrench with two loads acting on it. a nut is at point c and the forces are acting on the other end

Given:
Wrench shown below with two forces acting upon it
Determine:
the combined moment for both forces about point C

Solution:
In order to simplify the solution, begin by considering only one force at a time with C as the center of moments. In order to do this, consider that a moment is defined as the product of a force and a specific perpendicular distance. Find the moment for each force separately. The 100 pound force has a moment arm (perpendicular distance from line of action to the center of moments) of 12 inches. Therefore, the moment caused by this force equals

(100 pounds)(12 in) = 1200 pound-inches

The moment arm for the 200 pound force is zero because the line of action of the force passes through C. So the moment caused by the 200 pound force is

(200 pounds)(0 inches) = 0 pound-inches

In order to find the combined moment of the two forces, simply add their individual moments or

1200 pound-inches + 0 pound-inches = 1200 pound-inches
The moment resulting from these two forces can be taken about any point, not just the nut around which the wrench is physically turning. Take point A and repeat the above proceedure. The solution will be (100 pounds)(8inches) = 800 pound-inches and (200 pounds)(3inches) = 600 pound-inches. The total combined moment about point A which will be 800 pound-inches + 600 pound-inches = 1400 pound-inches

What is the total combined moment about point B?

Lecture 5 Example Problem

Lecture 5
Example Problem