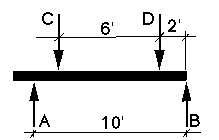
Given: a beam with the geometry and loading indicated (C = 3200 pounds and D = 1500 pounds)Solution: Moments can be used to determine the reactions at the ends of simple beams. Either point A or point B could be chosen as the center of moments. Since the exercise indicated that B is the center of moments, the first step is to determine all of the loads that will tend to cause a counter-clockwise rotation about B. These loads are placed on the left side of an equation and all of the loads which will tend to cause a clockwise rotation will be placed on the right side. The 1500 pound and the 3200 pound loads cause counter-clockwise rotations. The reaction at A is the only load that causes a clockwise rotation to the beam. Notice that the reaction at B does not even come into consideration. Why is this?
(1500 pounds)(2 feet ) + (3200 pounds)(8 feet) = A x 10 feet
3000 pound-feet + 25600 pound-feet = A x 10 feet
This yields a reaction of 2860 pounds at point A.
Try this if point A had been chosen as the center of moments. What is the reaction at B?