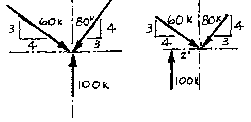Given:
Solution:
We note that the system on the left is a concurrent system and the one on the right is a non-concurrent, non-parallel system. In order for either system to be in equilibrium, all three equations of equilibrium,
Sum Fx = 0,
Sum Fy = 0 and
Sum M = 0 must be satisfied.
Begin by determining if the sum of the forces in the vertical and horizontal directions are equal to zero. The simplest way to solve these two systems would be to break each of the diagonal forces into their vertical and horizontal component parts. One can utilize trigonometry functions for this or, from observation, each diagonal is the "5" side of a 3-4-5 triangle. Therefore, the side marked "3" has a value of 3/5 of the value of the diagonal and the side marked "4" is equal to 4/5 the value of the diagonal.
Now, using the components, solve for the sum of forces equations.
Now solve for the sum of moments equation. The system on the left is in moment equilibrium because it is a concurrent force system. Take the sum of the moments at their point of intersection. For each force, the moment arm is equal to zero. Once equilibrium has been established using this single point, the sum of the moments for that force system will be zero for any point on that plane.
The force system on the right is not in moment equilibrium. Taking the sum of moments around the same point as before, the moment arm of the two diagonal forces are zero, but the 100 pound force will cause a clockwise rotation. This system cannot be put into equilibrium with a single force because that would disrupt the sum of forces equations. The easiest solution would be an applied moment, equal in magnitude to that caused by the 100 pound force, but opposite in sense.