The Principle of Moments

The Principle of Moments, also known as Varignon's Theorem, states that the moment of any force is equal to the algebraic sum of the moments of the components of that force. It is a very important principle that is often used in conjunction with the Principle of Transmissibility in order to solve systems of forces that are acting upon and/or within a structure. This concept will be illustrated by calculating the moment around the bolt caused by the 100 pound force at points A, B, C, D, and E in the illustration.

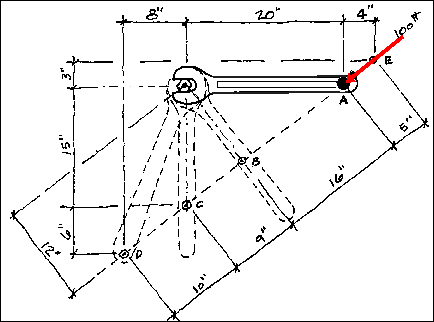
Lecture 10

First consider the 100 pound force
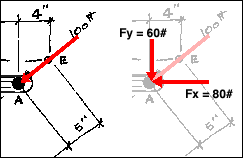
wrench
Since the line of action of the force is not perpendicular to the wrench at A, the force is broken down into its orthagonal components by inspection. The line of action of the the 100 pound force can be inspected to determine if there are any convenient geometries to aid in the decomposition of the 100 pound force. The 4 inch horizontal and the 5 inch diagonal measurement near point A should be recognized as belonging to a 3-4-5 triangle. Therefore, Fx = -4/5(100 pounds) or -80 pounds and Fy = -3/5(100 pounds) or -60 pounds.

Consider Point A
The line of action of F_x at A passes through the handle of the wrench to the bolt (which is also the center of moments). This means that the magnitude of the moment arm is zero and therefore the moment due to FAx is zero. FAy at A has a moment arm of twenty inches and will tend to cause a positive moment.

FAy d = (60 pounds)(20in) = 1200 pound-inches or 100 pound-feet

The total moment caused by the 100 pound force F at point A is 1200 pound-inches.

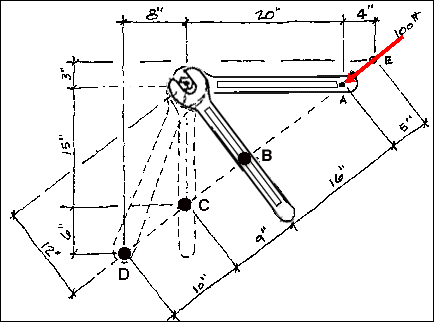wrench Consider Point B
At this point the 100 pound force is perpendicular to the wrench. Thus, the total moment due to the force can easily be found without breaking it into components.

FB d = (100 pounds)(12in) = 1200 pound-inches

The total moment caused by the 100 pound force F at point B is again 1200 pound-inches.

Consider Point C
The force must once again be decomposed into components. This time the vertical component passes through the center of moments. The horizontal component FCx causes the entire moment.

FCx d = (80 pounds)(15inches) = 1200 pound-inches

Consider Point D.
The force must once again be decomposed into components. Both components will contribute to the total moment.

FDx d = (80 pounds)(21inches) = 1680 pound-inches
FDy d = (60 pounds)(8in) = -480 pound-inches

Note that the y component in this case would create a counterclockwise or negative rotation. The total moment at D due to the 100 pound force is determined by adding the two component moments. Not surprisingly, this yields 1200 pound-inches.

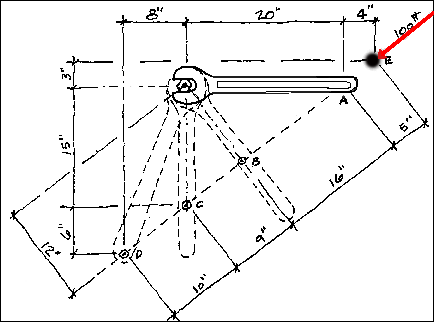
wrench
Consider Point E
Varignon's Theorem applies even though point E is removed from the physical object. Following the same procedure as at point D;

FEx d = (80 pounds)(3in) = -240 pound-inches
FEy d = (60 pounds)(24in) = 1440 pound-inches

However, this time Fx tends to cause a negative moment. Once again the total moment is 1200 pound-inches.

Summary for the example At each point, A, B, C, D and E the total moment around the bolt caused by the 100 pound force equalled 1200 pound-inches. In fact, the total moment would equal 1200 pound-inches at ANY point along the line of action of the force. This is Varignon's Theorem.

Questions for Thought

Homework Problems

Additional Reading