 What are Couples?
What are Couples? What are Couples?
What are Couples?
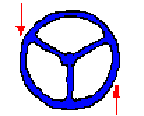
A special case of moments is a couple. A couple consists of two parallel forces that are equal in magnitude, opposite in sense and do not share a line of action. It does not produce any translation, only rotation. The resultant force of a couple is zero. BUT, the resultant of a couple is not zero; it is a pure moment.
For example, the forces that two hands apply to turn a steering wheel are often (or should be) a couple. Each hand grips the wheel at points on opposite sides of the shaft. When they apply a force that is equal in magnitude yet opposite in direction the wheel rotates. If both hands applied a force in the same direction, the sum of the moments created by each force would equal zero and the wheel would not rotate. Instead of rotating around the shaft, the shaft would be loaded with a force tending to cause a translation with a magnitude of twice F. If the forces applied by the two hands were unequal, there would again be an unbalanced force creating a translation of the "system." A pure couple always consists of two forces equal in magnitude.
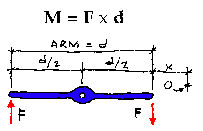
The moment of a couple is the product of the magnitude of one of the forces and the perpendicular distance between their lines of action. M = F x d. It has the units of kip-feet, pound-inches, KN-meter, etc. The magnitude of the moment of a couple is the same for all points in the plane of the couple. A couple may be moved anywhere in its plane or a parallel plane without changing its external effect. The magnitude of the couple is independent of the reference point and its tendency to create a rotation will remain constant. This can be illustrated with the simple illustration of a bar with a length d that is pinned at its midpoint. Two parallel forces of equal magnitude, opposite in sense are applied at the ends of the bar. The magnitude of the moment generated by the couple of the forces F, relative to the pin in the illustration, is equal to
(F)(d/2) + (F)(d/2)
= (F)(d)
The magnitude of the couple of the forces F relative to point "O" is
(F)(d+x) - (F)(x)
(F)(d) + (F)(x) - (F)(x)
= (F)(d)
Again, it can be seen that the magnitude of the couple is independent of the reference location. It is always equal to (F)(d)!
The resultant of a number of couples is their algebraic sum. A couple CANNOT be put in equilibrium by a single force! A couple can only be put in equilibrium by a moment or another couple of equal magnitude and opposite direction anywhere in the same plane or in a parallel plane. If a single force is added to the system that balances the sum of the moments, one of the other two equations of equilibrium will not be satisfied. A couple maintains the internal equilibrium of a simple beam or of many other simple structural systems. The concept is very important to the further study of structural behaviour.
There are many examples of couples in the built world. Some structures
are clear manifestations of the couple; others hide the couple inside oftheir
structural elements.
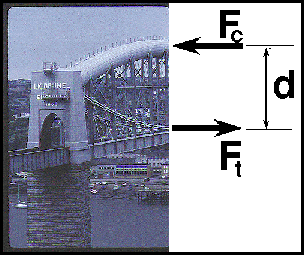
The Saltash Bridge by Brunel is a structure which allows the couple at midspan
to be clearly read. The structure illustrates the equilibrium developed
by the compressive force of the top chord and the equal and opposite tensile
force of the suspension chain. These two forces create a couple at midspan.
The magnitude of the couple would be the force Fc or Ft
times the distance seperating the two forces, d. This is the same
type of couple that is hidden inside of solid beams.
Would the magnitude of the couple change as a train rolled over the bridge?
Why or Why not? 
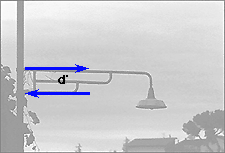
Here is an example of a common street lamp. The lamp creates a moment
with the magnitude determined by the weight of the lamp times the moment
arm,d. This moment is resisted by a couple generated by the tubes of the
supporting arm. The two forces of the couple can be seen in the compression
and tension forces that are seperated by a much smaller distance. These
act to put the system back into equilibrium.
What other forces are required to keep the system in equilibrium?

hmmm.....
when found....