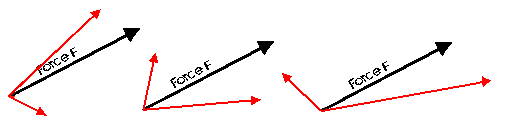
The Elements of Coplanar Force Resolution
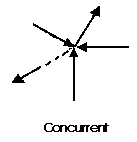
A concurrent coplanar force system is a system of two or more forces
whose lines of action ALL intersect at a common point. However, all of the
individual vectors might not acutally be in contact with the common point.
These are the most simple force systems to resolve with any one of many
graphical or algebraic options.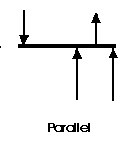 
A parallel coplanar force system consists of two or more forces whose
lines of action are ALL parallel. This is commonly the situation when simple
beams are analyzed under gravity loads. These can be solved graphically,
but are combined most easily using algebraic methods.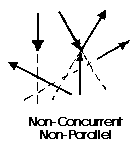 
The last illustration is of a non-concurrent and non-parallel system.
This consists of a number of vectors that do not meet at a single point
and none of them are parallel. These systems are essentially a jumble of
forces and take considerable care to resolve.
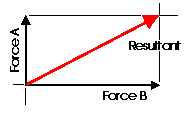Almost any system of known
forces can be resolved into a single force called a resultant force or simply
a Resultant. The resultant is a representative force which has the
same effect on the body as the group of forces it replaces. (A couple is
an exception to this) It, as one single force, can represent any number
of forces and is very useful when resolving multiple groups of forces. One
can progressively resolve pairs or small groups of forces into resultants.
Then another resultant of the resultants can be found and so on until all
of the forces have been combined into one force. This is one way to save
time with the tedious "bookkeeping" involved with a large number
of individual forces. Resultants can be determined both graphically and
algebraically. The graphical methods that will be discussed in Lecture 8 are the Parallelogram Method
and the Triangle Method. It is important to note that for any given system
of forces, there is only one resultant.
It is often
convenient to decompose a single force into two distinct forces. These forces,
when acting together, have the same external effect on a body as the original
force. They are known as components. Finding the components of a
force can be viewed as the converse of finding a resultant. There are an
infinate number of components to any single force. And, the correct choice
of the pair to represent a force depends upon the most convenient geometry.
For simplicity, the most convenient is often the coordinate axis of a structure.
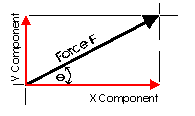This diagram illustrates a
pair of components that correspond with the X and Y axis. These are known
as the rectangular components of a force. Rectangular components
can be thought of as the two sides of a right angle which are at ninety
degrees to each other. The resultant of these components is the hypotenuse
of the triangle. The rectangular components for any force can be found with
trigonometrical relationships: Fx = F cos theta, Fy
= F sin theta (where theta is the angle). There are a few geometric relationships
that seem common in general building practice in North America. These relationships
relate to roof pitches, stair pitches, and common slopes or relationships
between truss members. Some of these are triangles with sides of ratios
of 3-4-5, 1-2-sqrt3, 1-1-sqrt2, 5-12-13 or 8-15-17. Commiting the first
three to memory will simplify the determination of vector magnitudes when
resolving more difficult problems.
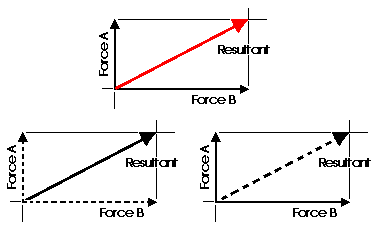
When forces are being represented as vectors, it is important to should
show a clear distinction between a resultant and its components. The resultant
could be shown with color or as a dashed line and the components as solid
lines, or vice versa. NEVER represent the resultant in the same graphic
way as its components.
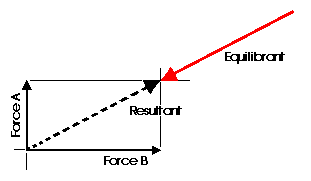
Any concurrent set of forces, not in equilibrium, can be put into a state
of equilibrium by a single force. This force is called the Equilibrant.
It is equal in magnitude, opposite in sense and co-linear with the resultant.
When this force is added to the force system, the sum of all of the forces
is equal to zero. A non-concurrent or a parallel force system can actually
be in equilibrium with respect to all of the forces, but not be in equilibrium
with respect to moments.
Graphic Statics and graphical methods of force resolution were developed before the turn of the century by Karl Culmann. They were the only methods of structural analysis for many years. These methods can help to develop an intuitive understanding of the action of the forces. Today, the Algebraic Method is considered to be more applicable to structural design. Despite this, graphical methods are a very easy way to get a quick answer for a structural design problem and can aid in the determination of structural form.
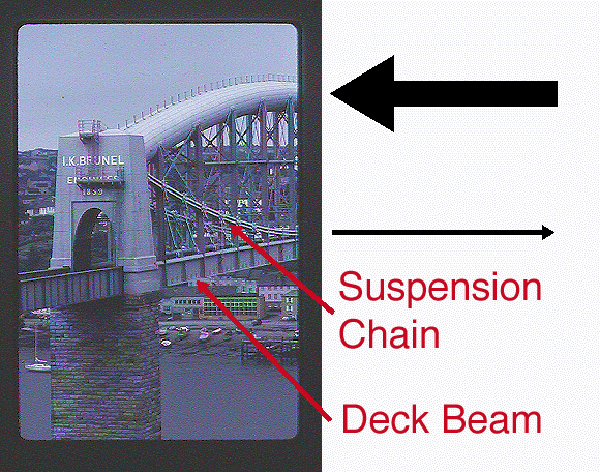
The following is an example of how an understanding of structural action
and force resolution can aid in the interpretation of structural form. The
illustration on the left is the Saltash Bridge, design and built by the
Engineer Brunel in 1859. Notice the form of the structural elements. The
illustration on the right is a retouched imaged to bring the bridge to a
state which is akin to a pure suspension bridge. However, there are some issues
with this design that need to be clearly understood.
Since this is a railroad bridge, trains of various weights will rumble across.
The weight of the train is carried by the horizontal deck which is within the space defined by
the steel girders. These girders are supported by hangers which extend from
the chain to the girder. Each one of these hangers is loaded in pure vertical tension. The suspension
chain is loaded with a vertical load as the deck is loaded with a train.
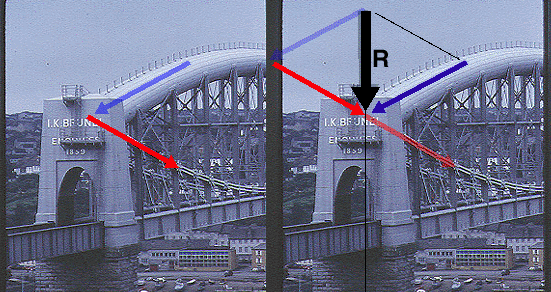
This action would tend to cause the chain to pull the towers towards the middle
of the river. This can be clearly seen if one resolves the tension force
into its two orthagonal components. The system is not in equilibrium without some force to resist the lateral
component of the resolution.
The system is usually put back into equilibrium by the additional tension
force of a chain, or cable, continuing over the supporting pylon to an anchor on
the bank of the river. This was not possible here. Thus, instead of a tensile force,
Brunel resisted the lateral component with a compressive
thrust which was created by the massive arch. In the illustration below this is seen as
the large black arrow. The chain link suspension system works in harmony
with the arch....
An examination of the resolution of the forces at the support MUST reveal
that the resultant passes through the stone pillar.....which it does.
Components
of Forces and Equilibrium
What would be other options for the Saltash bridge now that over a century has passed since it's desgin? What could/would be the most likely location for a strength or stability failure of the bridge? What might the design implication be if the chain was replaced by a wire rope?
Shaeffer, R. E. Elementary Structures for Architects and Builders.
pp. 21-33.
Allen, Ed. Graphic Statics.