Algebraic Methods of Coplanar Force Resolution
The solution of many problems is greatly simplified by using the rectangular components. These are usually noted as Fx, for forces parallel to the X axis, and Fy, for forces parallel to the Y axis. They are also known simply as H, for horizontal, and V, for vertical.
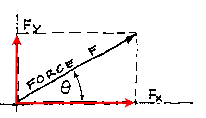
The rectangular components may be determined graphically, where the force is shown as a vector, or algebraically. In order to resolve a vector into its components, Fx = F cos or Fy = F sin , one must know at least two items of the six geometric descriptors of a triangle (the lengths of the sides and the three angles).
Conversely, if the magnitude of the rectangular components are known, the resultant can be found with the Pythagorean Theorem, F = SQRT (Fx^2 + Fy^2). The direction of the resultant may be determined by trigonometry knowing that the tan is = opposite side / adjacent side.
The solutions to many problems are greatly simplified by resolving multiple forces into a resultant or by finding the rectangular components of a force system. This tool will be used extensively throughout the course.
In summary:
Fx = F cos
Fy = F sin
F = SQRT (Fx^2 + Fy^2)
tan = Fx / Fy = opposite side / adjacent side
The resultant of any number of concurrent forces can be found by resolving
each force into its rectangular components and then adding the components
algebraically. Remember, the sum of Fx = 0 and Fy = 0. The resulting numbers will be the compontents of
the resultant. From these, the resultant can be found as before by using
the Pythagorean Theorem in which R = SQRT (Fx^2 + Fy^2) and the formula for tan = Fy
/ Fx.
Algebraic Method of Resolving Concurrent Coplanar Forces
Unlike coplanar, concurrent force systems, Parallel Force Systems cannot be completely resolved using the methods described above. Remember that every force is defined to have a magnitude, a direction and a line of action. The magnitude of the resultant of a parallel force system is equal to the algebraic sum of the components. This can also establish the resultant's direction and sense, but not its line of action. In order to find the resulatant's point of application another principle of equilibrium must be utilized: the moment of the resultant about any point is equal to the moment of the components about the same point. This principle is very useful for resolving multiple groupings of forces into a single force in order to simplify the calculation of reactions at the supports of a member or structure. This is best illustrated with the following example.
Algebraic Resolution of a Parallel Force System
coming....
TBA