#### Software in 6.005
| Safe from bugs | Easy to understand | Ready for change |
|---|
|
Correct today and correct in the unknown future.
|
Communicating clearly with future programmers, including future you.
|
Designed to accommodate change without rewriting.
|
#### Objectives
Today's reading introduces several ideas:
+ abstraction functions
+ representation invariants
+ equality
+ the Object contract
In this reading, we study a more formal mathematical idea of what it means for a class to implement an ADT, via the notions of *abstraction functions* and *rep invariants*. These mathematical notions are eminently practical in software design. The abstraction function will give us a way to cleanly define the equality operation on an abstract data type, and the rep invariant will make it easier to catch bugs caused by a corrupted data structure.
## Rep Invariant and Abstraction Function
We now take a deeper look at the theory underlying abstract data types. This theory is not only elegant and interesting in its own right; it also has immediate practical application to the design and implementation of abstract types. If you understand the theory deeply, you'll be able to build better abstract types, and will be less likely to fall into subtle traps.
In thinking about an abstract type, it helps to consider the relationship between two spaces of values.
The space of representation values (or rep values for short) consists of the values of the actual implementation entities. In simple cases, an abstract type will be implemented as a single object, but more commonly a small network of objects is needed, so this value is actually often something rather complicated. For now, though, it will suffice to view it simply as a mathematical value.
The space of abstract values consists of the values that the type is designed to support. These are a figment of our imaginations. They're platonic entities that don't exist as described, but they are the way we want to view the elements of the abstract type, as clients of the type. For example, an abstract type for unbounded integers might have the mathematical integers as its abstract value space; the fact that it might be implemented as an array of primitive (bounded) integers, say, is not relevant to the user of the type.
Now of course the implementor of the abstract type must be interested in the representation values, since it is the implementor's job to achieve the illusion of the abstract value space using the rep value space.
Suppose, for example, that we choose to use a string to represent a Set<Character>.
```java
public class CharSet implements Set<Character> {
private String s;
...
}
```
Then the rep space R contains Strings, and the abstract space A is mathematical sets of characters. We can show the two value spaces graphically, with an arc from a rep value to the abstract value it represents. There are several things to note about this picture:
+ **Every abstract value is mapped to by some rep value**. The purpose of implementing the abstract type is to support operations on abstract values. Presumably, then, we will need to be able to create and manipulate all possible abstract values, and they must therefore be representable.
+ **Some abstract values are mapped to by more than one rep value**. This happens because the representation isn't a tight encoding. There's more than one way to represent an unordered set of characters as a string.
+ **Not all rep values are mapped**. In this case, the string "abbc" is not mapped. In this case, we have decided that the string should not contain duplicates. This will allow us to terminate the remove method when we hit the first instance of a particular character, since we know there can be at most one.
In practice, we can only illustrate a few elements of the two spaces and their relationships; the graph as a whole is infinite. So we describe it by giving two things:
1\. An *abstraction function* that maps rep values to the abstract values they represent:
> AF : R → A
The arcs in the diagram show the abstraction function. In the terminology of functions, the properties we discussed above can be expressed by saying that the function is surjective (also called *onto*), not necessarily bijective (also called *one-to-one*), and often partial.
2\. A *rep invariant* that maps rep values to booleans:
> RI : R → boolean
For a rep value r, RI(r) is true if and only if r is mapped by AF. In other words, RI tells us whether a given rep value is well-formed. Alternatively, you can think of RI as a set: it's the subset of rep values on which AF is defined.
Both the rep invariant and the abstraction function should be documented in the code, right next to the declaration of the rep itself:
```java
public class CharSet_NoRepeatsRep implements Set<Character> {
private String s;
// Rep invariant:
// s contains no repeated characters
// Abstraction Function:
// represents the set of characters found in s
...
}
```
A common confusion about abstraction functions and rep invariants is that they are determined by the choice of rep and abstract value spaces, or even by the abstract value space alone. If this were the case, they would be of little use, since they would be saying something redundant that's already available elsewhere.
The abstract value space alone doesn't determine AF or RI: there can be several representations for the same abstract type. A set of characters could equally be represented as a string, as above, or as a bit vector, with one bit for each possible character. Clearly we need two different abstraction functions to map these two different rep value spaces.
It's less obvious why the choice of both spaces doesn't determine AF and RI. The key point is that defining a type for the rep, and thus choosing the values for the space of rep values, does not determine which of the rep values will be deemed to be legal, and of those that are legal, how they will be interpreted. Rather than deciding, as we did above, that the strings have no duplicates, we could instead allow duplicates, but at the same time require that the characters be sorted, appearing in nondecreasing order. This would allow us to perform a binary search on the string and thus check membership in logarithmic rather than linear time. Same rep value space -- different rep invariant:
```java
public class CharSet_SortedRep implements Set<Character> {
private String s;
// Rep invariant:
// s[0] < s[1] < ... < s[s.length()-1]
// Abstraction Function:
// represents the set of characters found in s
...
}
```
Even with the same type for the rep value space and the same rep invariant RI, we might still interpret the rep differently, with different abstraction functions AF. Suppose RI admits any string of characters. Then we could define AF, as above, to interpret the array's elements as the elements of the set. But there's no *a priori* reason to let the rep decide the interpretation. Perhaps we'll interpret consecutive pairs of characters as subranges, so that the string "acgg" represents the set {a,b,c,g}.
```java
public class CharSet_SortedRangeRep implements Set<Character> {
private String s;
// Rep invariant:
// s.length is even
// s[0] <= s[1] <= ... <= s[s.length()-1]
// Abstraction Function:
// represents the union of the ranges
// {s[i]...s[i+1]} for each adjacent pair of characters
// in s
...
}
```
The essential point is that designing an abstract type means **not only choosing the two spaces** -- the abstract value space for the specification and the rep value space for the implementation -- **but also deciding what rep values to use and how to interpret them**.
It's critically important to write down these assumptions in your code, as we've done above, so that future programmers (and your future self) are aware of what the representation actually means. Why? What happens if different implementers disagree about the meaning of the rep?
mitx:b4aeda0673304efd839e6fab6d89ded3 AF and RI
### Example: Rational Numbers
Here's an example of an abstract data type for rational numbers. Look closely at its rep invariant and abstraction function.
```java
public class RatNum {
private final int numer;
private final int denom;
// Rep invariant:
// denom > 0
// numer/denom is in reduced form
// Abstraction Function:
// represents the rational number numer / denom
/** Make a new Ratnum == n. */
public RatNum(int n) {
numer = n;
denom = 1;
checkRep();
}
/**
* Make a new RatNum == (n / d).
* @param n numerator
* @param d denominator
* @throws ArithmeticException if d == 0
*/
public RatNum(int n, int d) throws ArithmeticException {
// reduce ratio to lowest terms
int g = gcd(n, d);
n = n / g;
d = d / g;
// make denominator positive
if (d < 0) {
numer = -n;
denom = -d;
} else {
numer = n;
denom = d;
}
checkRep();
}
}
```
Here is a picture of the abstraction function and rep invariant for this code. The RI requires that numerator/denominator pairs be in reduced form (i.e., lowest terms), so pairs like (2,4) and (18,12) above should be drawn as outside the RI.
It would be completely reasonable to design another implementation of this same ADT with a more permissive RI. With such a change, some operations might become more expensive to perform, and others cheaper.
### Checking the Rep Invariant
The rep invariant isn't just a neat mathematical idea. If your implementation asserts the rep invariant at run time, then you can catch bugs early. Here's a method for RatNum that tests its rep invariant:
```java
// Check that the rep invariant is true
// *** Warning: this does nothing unless you turn on assertion checking
// by passing -enableassertions to Java
private void checkRep() {
assert denom > 0;
assert gcd(numer, denom) == 1;
}
```
You should certainly call checkRep() to assert the rep invariant at the end of every operation that creates or mutates the rep -- in other words, creators, producers, and mutators. Look back at the RatNum code above, and you'll see that it calls checkRep() at the end of both constructors.
Observer methods don't normally need to call checkRep(), but it's good defensive practice to do so anyway. Why? Calling checkRep() in every method, including observers, means you'll be more likely to catch rep invariant violations caused by rep exposure.
Why is checkRep private? Who should be responsible for checking and enforcing a rep invariant -- clients, or the implementation itself?
### No Null Values in the Rep
Recall from the [specs reading](../06-specifications/specs) that null values are troublesome and unsafe, so much so that we try to remove them from our programming entirely.
In 6.005, the preconditions and postconditions of our methods implicitly require that objects and arrays be non-null.
We extend that prohibition to the reps of abstract data types. By default, in 6.005, the rep invariant implicitly includes `x != null` for every reference `x` in the rep that has object type (including references inside arrays or lists). So if your rep is:
```java
class CharSet {
String s;
}
```
then its rep invariant automatically includes `s != null`, and you don't need to state it in a rep invariant comment.
When it's time to implement that rep invariant in a checkRep() method, however, you still must *implement* the `s != null` check, and make sure that your checkRep() correctly fails when `s` is `null`. Often that check comes for free from Java, because checking other parts of your rep invariant will throw an exception if `s` is null. For example, if your checkRep() looks like this:
```java
private void checkRep() {
assert s.length() % 2 == 0;
...
}
```
then you don't need `assert s!= null`, because the call to `s.length()` will fail just as effectively on a null reference. But if `s` is not otherwise checked by your rep invariant, then assert `s != null` explicitly.
mitx:66dd1e7b3e854213992dde2cdd21a859 Checking the Rep Invariant
## Equality
Now we turn to how we define the notion of equality of values in a data type.
In the physical world, every object is distinct -- at some level, even two snowflakes are different, even if the distinction is just the position they occupy in space. (This isn't strictly true of all subatomic particles, actually, but true enough of large objects like snowflakes and baseballs and people.) So two physical objects are never truly "equal" to each other; they only have degrees of similarity.
In the world of human language, however, and in the world of mathematical concepts, you can have multiple names for the same thing. So it's natural to ask when two expressions represent the same thing: 1+2, √9, and 3 are alternative expressions for the same ideal mathematical value.
### Three Ways to Regard Equality
Formally, we can regard equality in several ways.
**Using an abstraction function**. Recall that an abstraction function f: R → A maps concrete instances of a data type to their corresponding abstract values. To use f as a definition for equality, we would say that a equals b if and only if f(a)=f(b).
**Using a relation**. An *equivalence* is a relation E ⊆ T x T that is:
+ reflexive: E(t,t) ∀ t ∈ T
+ symmetric: E(t,u) ⇒ E(u,t)
+ transitive: E(t,u) ∧ E(u,v) ⇒ E(t,v)
To use E as a definition for equality, we would say that a equals b if and only if E(a,b).
These two notions are equivalent. An equivalence relation induces an abstraction function (the relation partitions T, so f maps each element to its partition class). The relation induced by an abstraction function is an equivalence relation (check for yourself that the three properties hold).
A third way we can talk about the equality between abstract values is in terms of what an outsider (a client) can observe about them:
**Using observation**. We can say that two objects are equal when they cannot be distinguished by observation -- every operation we can apply produces the same result for both objects. Consider the set expressions {1,2} and {2,1}. Using the observer operations available for sets, cardinality |...| and membership ∈, these expressions are indistinguishable:
+ |{1,2}| = 2 and |{2,1}| = 2
+ 1 ∈ {1,2} is true, and 1 ∈ {2,1} is true
+ 2 ∈ {1,2} is true, and 2 ∈ {2,1} is true
+ 3 ∈ {1,2} is false, and 3 ∈ {2,1} is false
+ ... and so on
In terms of abstract data types, "observation" means calling operations on the objects. So two objects are equal if and only if they cannot be distinguished by calling any operations of the abstract data type.
### Example: Duration
Here's a simple example of an immutable ADT.
```java
public class Duration {
private final int mins;
private final int secs;
// rep invariant:
// mins >= 0, secs >= 0
// abstraction function:
// represents a span of time of mins minutes and secs seconds
/** Make a duration lasting for m minutes and s seconds. */
public Duration(int m, int s) {
mins = m; secs = s;
}
/** @return length of this duration in seconds */
public long getLength() {
return mins*60 + secs;
}
}
```
Now which of the following values should be considered equal?
```java
Duration d1 = new Duration (1, 2);
Duration d2 = new Duration (1, 3);
Duration d3 = new Duration (0, 62);
Duration d4 = new Duration (1, 2);
```
Think in terms of both the abstraction-function definition of equality, and the observational equality definition.
mitx:656052a10662494f87d5fd13d62a3abc Equality
### == vs. equals()
Like many languages, Java has two different operations for testing equality, with different semantics.
+ The == operator compares references. More precisely, it tests *referential* equality. Two references are == if they point to the same storage in memory. In terms of the snapshot diagrams we've been drawing, two references are == if their arrows point to the same object bubble.
+ The equals() operation compares object contents -- in other words, *object* equality, in the sense that we've been talking about in this reading. The equals operation has to be defined appropriately for every abstract data type.
For comparison, here are the equality operators in several languages:
|
|
*referential
equality*
|
*object
equality*
|
|
Java
|
`==`
|
`equals()`
|
|
Objective C
|
`==`
|
`isEqual:`
|
|
C#
|
`==`
|
`Equals()`
|
|
Python
|
`is`
|
`==`
|
|
Javascript
|
`==`
|
n/a
|
Note that == unfortunately flips its meaning between Java and Python. Don't let that confuse you: == in Java just tests reference identity, it doesn't compare object contents.
As programmers in any of these languages, we can't change the meaning of the referential equality operator. In Java, == always means referential equality. But when we define a new data type, it's our responsibility to decide what object equality means for values of the data type, and implement the equals() operation appropriately.
The equals() method is defined by Object, and its default implementation looks like this:
```java
public class Object {
...
public boolean equals (Object that) {
return this == that;
}
}
```
In other words, the default meaning of equals() is the same as referential equality. For immutable data types, this is almost always wrong. So you have to **override** the equals() method, replacing it with your own implementation.
Here's our first try for Duration:
```java
public class Duration {
...
// Problematic definition of equals()
public boolean equals(Duration that) {
return this.getLength() == that.getLength();
}
}
```
There's a subtle problem here. Why doesn't this work? Let's try this code:
```java
Duration d1 = new Duration (1, 2);
Duration d2 = new Duration (1, 2);
Object o2 = d2;
d1.equals(d2) → true
d1.equals(o2) → false
```
What's going on? It turns out that Duration has **overloaded** the equals() method, because the method signature was not identical to Object's. We actually have two equals() methods in Duration: an implicit equals(Object) inherited from Object, and the new equals(Duration).
```java
public class Duration extends Object {
// explicit method that we declared:
public boolean equals (Duration that) {
return this.getLength() == that.getLength();
}
// implicit method inherited from Object:
public boolean equals (Object that) {
return this == that;
}
}
```
Recall from an earlier reading that the compiler selects between overloaded operations using the compile-time type of the parameters. For example, when you use the `/` operator, the compiler chooses either integer division or float division based on whether the arguments are ints or floats. The same compile-time selection happens here. If we pass an Object reference, as in `d1.equals(o2)`, we end up calling the equals(Object) implementation. If we pass a Duration reference, as in `d1.equals(d2)`, we end up calling the equals(Duration) version. This happens even though `o2` and `d2` both point to the same object at runtime! Equality has become inconsistent.
It's easy to make a mistake in the method signature, and overload a method when you meant to override it. This is such a common error that Java has a language feature, the annotation @Override, which you should use whenever your intention is to override a method in your superclass. With this annotation, the Java compiler will check that a method with the same signature actually exists in the superclass, and give you a compiler error if you've made a mistake in the signature.
So here's the right way to implement Duration's equals() method:
```java
@Override
public boolean equals (Object thatObject) {
if (!(thatObject instanceof Duration)) return false;
Duration thatDuration = (Duration) thatObject;
return this.getLength() == thatDuration.getLength();
}
```
This fixes the immediate problem:
```java
Duration d1 = new Duration(1, 2);
Object o2 = new Duration(1,2);
d1.equals(o2) → true
o2.equals(d1) → ?? // is it symmetric?
```
## The Object Contract
The specification of the Object class is so important that it is often referred to as *the Object Contract*. The contract can be found in the method specifications for the Object class. Here we will focus on the contract for equals. When you override the equals method, you must adhere to its general contract. It states that:
+ equals must define an equivalence relation -- that is, a relation that is reflexive, symmetric, and transitive;
+ equals must be consistent: repeated calls to the method must yield the same result provided no information used in equals comparisons on the object is modified;
+ for a non-null reference x, x.equals (null) should return false;
+ hashCode must produce the same result for two objects that are deemed equal by the equals
method.
### Breaking the Equivalence Relation
Let's start with the equivalence relation. We have to make sure that the definition of equality implemented by equals() is actually an equivalence relation as defined earlier: reflexive, symmetric, and transitive. If it isn't, then operations that depend on equality (like sets, searching) will behave erratically and unpredictably. You don't want to program with a data type in which sometimes a equals b, but b doesn't equal a. Subtle and painful bugs will result.
Here's an example of how an innocent attempt to make equality more flexible can go wrong. Suppose we wanted to allow for a tolerance in comparing Durations, because different computers may have slightly unsynchronized clocks:
```java
private static final int CLOCK_SKEW = 5; // seconds
@Override
public boolean equals (Object thatObject) {
if (!(thatObject instanceof Duration)) return false;
Duration thatDuration = (Duration) thatObject;
return Math.abs(this.getLength() - thatDuration.getLength()) <= CLOCK_SKEW;
}
```
Which property of the equivalence relation is violated?
mitx:260a89898fae4bb4baa7fea8fdca84e8 Equivalence Properties
### Breaking Hash Tables
To understand the part of the contract relating to the hashCode method, you'll need to have some idea of how hash tables work. Two very common collection implementations, HashSet and HashMap, use a hash table data structure, and depend on the hashCode method to be implemented correctly for the objects stored in the set and used as keys in the map.
A hash table is a representation for a mapping: an abstract data type that maps keys to values. Hash tables offer constant time lookup, so they tend to perform better than trees or lists. Keys don't have to be ordered, or have any particular property, except for offering equals and hashCode.
Here's how a hash table works. It contains an array that is initialized to a size corresponding to the number of elements that we expect to be inserted. When a key and a value are presented for insertion, we compute the hashcode of the key, and convert it into an index in the array's range (e.g., by a modulo division). The value is then inserted at that index.
The rep invariant of a hash table includes the fundamental constraint that keys are in the slots determined by their hash codes.
Hashcodes are designed so that the keys will be spread evenly over the indices. But occasionally a conflict occurs, and two keys are placed at the same index. So rather than holding a single value at an index, a hash table actually holds a list of key/value pairs, usually called a *hash bucket*. A key/value pair is implemented in Java simply as an object with two fields. On insertion, you add a pair to the list in the array slot determined by the hash code. For lookup, you hash the key, find the right slot, and then examine each of the pairs until one is found whose key matches the query key.
Now it should be clear why the Object contract requires equal objects to have the same hashcode. If two equal objects had distinct hashcodes, they might be placed in different slots. So if you attempt to lookup a value using a key equal to the one with which it was inserted, the lookup may fail.
Object's default hashCode() implementation is consistent with its default equals():
```java
public class Object {
...
public boolean equals(Object that) { return this == that; }
public int hashCode() { return /* the address of this */; }
}
```
For references a and b, if a == b, then the address of a == the address of b. So the Object contract is satisfied.
But immutable objects need a different implementation of hashCode(). For Duration, since we haven't overridden the default hashCode() yet, we're currently breaking the Object contract:
```java
Duration d1 = new Duration(1,2);
Duration d2 = new Duration(1,2);
d1.equals(d2) → true
d1.hashCode() → 2392
d2.hashCode() → 4823
```
d1 and d2 are equal(), but they have different hash codes. So we need to fix that.
A simple and drastic way to ensure that the contract is met is for hashCode to always return some constant value, so every object's hash code is the same. This satisfies the Object contract, but it would have a disastrous performance effect, since every key will be stored in the same slot, and every lookup will degenerate to a linear search along a long list.
The standard way to construct a more reasonable hash code that still satisfies the contract is to compute a hash code for each component of the object that is used in the determination of equality (usually by calling the hashCode method of each component), and then combining these, throwing in a few arithmetic operations. For Duration, this is easy, because the abstract value of the class is already an integer value:
```java
@Override
public int hashCode() {
return (int) getLength();
}
```
Josh Bloch's fantastic book, *Effective Java*, explains this issue in more detail, and gives some strategies for writing decent hash code functions. The advice is summarized in [a good StackOverflow post](http://stackoverflow.com/questions/113511/hash-code-implementation). Recent versions of Java now have a utility method [Objects.hash()](http://docs.oracle.com/javase/8/docs/api/java/util/Objects.html#hash-java.lang.Object...-) that makes it easier to implement a hash code involving multiple fields.
Note, however, that as long as you satisfy the requirement that equal objects have the same hash code value, then the particular hashing technique you use doesn't make a difference to the correctness of your code. It may affect its performance, by creating unnecessary collisions between different objects, but even a poorly-performing hash function is better than one that breaks the contract.
Most crucially, note that if you don't override hashCode at all, you'll get the one from Object, which is based on the address of the object. If you have overridden equals, this will mean that you will have almost certainly violated the contract. So as a general rule:
> **Always override hashCode when you override equals.**
Many years ago in 6.170, a student spent hours tracking down a bug in a project that amounted to nothing more than misspelling hashCode as hashcode. This created a new method that didn't override the hashCode method of Object at all, and strange things happened. Use @Override!
mitx:80e1e5e838d042559cbd04ee33920c6f Hash Codes
### Equality of Mutable Objects
We've been focusing on equality of immutable objects so far in this reading. What about mutable objects?
Recall our definition: two objects are equal when they cannot be distinguished by observation. With mutable objects, there are two ways to interpret this:
+ when they cannot be distinguished by observation *that doesn't change the state of the objects*, i.e., by calling only observer, producer, and creator methods. This is often strictly called **observational equality**, since it tests whether the two objects "look" the same, in the current state of the program.
+ when they cannot be distinguished by *any* observation, even state changes. This interpretation allows calling any methods on the two objects, including mutators. This is often called **behavioral equality**, since it tests whether the two objects will "behave" the same, in this and all future states.
For immutable objects, observational and behavioral equality are identical, because there aren't any mutator methods.
For mutable objects, it's tempting to implement strict observational equality. Java uses observational equality for most of its mutable data types, in fact. If two distinct List objects contain the same sequence of elements, then equals() reports that they are equal.
But using observational equality leads to subtle bugs, and in fact allows us to easily break the rep invariants of other collection data structures. Suppose we make a List, and then drop it into a Set:
```java
List<String> list = Arrays.asList(new String[] { "a" });
Set<List<String>> set = new HashSet<List<String>>();
set.add(list);
```
We can check that the set contains the list we put in it, and it does:
```java
set.contains(list) → true
```
But now we mutate the list:
```java
list.add("goodbye");
```
And it no longer appears in the set!
```java
set.contains(list) → false!
```
It's worse than that, in fact: when we iterate over the members of the set, we still find the list in there, but contains() says it's not there!
```java
for (List<String> l : set) {
set.contains(l) → false!
}
```
If the set's iterator and its contains() method disagree about whether an element is in the set, then the set clearly is broken.
What's going on? List<String> is a mutable object. In the standard Java implementation of collection classes like List, mutations affect the result of equals() and hashCode(). When the list is first put into the HashSet, it is stored in the hash bucket corresponding to its hashCode() result at that time. When the list is subsequently mutated, its hashCode() changes, but HashSet doesn't realize it should be moved to a different bucket. So it can never be found again.
When equals() and hashCode() can be affected by mutation, we can break the rep invariant of a hash table that uses that object as a key.
Here's a telling quote from the specification of java.util.Set:
> Note: Great care must be exercised if mutable objects are used as set elements. The behavior of a set is not specified if the value of an object is changed in a manner that affects equals comparisons while the object is an element in the set.
The Java library is unfortunately inconsistent about its interpretation of equals() for mutable classes. Collections use observational equality, but other mutable classes (like StringBuilder) use behavioral equality.
The lesson we should draw from this example is that **equals() should implement behavioral equality**. In general, that means that two references should be equal() if and only if they are aliases for the same object. So mutable objects should just inherit equals() and hashCode() from Object. For clients that need a notion of observational equality (whether two mutable objects "look" the same in the current state), it's better to define a new method, e.g., similar().
### The Final Rule for equals and hashCode()
**For immutable types**:
+ equals() should compare abstract values. This is the same as saying equals() should provide behavioral equality.
+ hashCode() should map the abstract value to an integer.
So immutable types **must** override both equals() and hashCode().
**For mutable types**:
+ equals() should compare references, just like ==. Again, this is the same as saying equals() should provide behavioral equality.
+ hashCode should map the reference into an integer.
So mutable types should not override equals() and hashCode() at all, and should simply use the default implementations provided by Object. Java doesn't follow this rule for its collections, unfortunately, leading to the pitfalls that we saw above.
mitx:5b0a43d1fedf49dfa95a07e5e0e1eaa3 Behavioral and Observational Equality
### Autoboxing and Equality
One more instructive pitfall in Java. We've talked about primitive types and their object type equivalents -- for example, int and Integer. The object type implements equals() in the correct way, so that if you create two Integer objects with the same value, they'll be equals() to each other:
```java
Integer x = new Integer(3);
Integer y = new Integer(3);
x.equals(y) → true
```
But there's a subtle problem here; == is overloaded. For reference types like Integer, it implements referential equality:
```java
x == y // returns false
```
But for primitive types like int, == implements behavioral equality:
```java
(int)x == (int)y // returns true
```
So you can't really use Integer interchangeably with int. The fact that Java automatically converts between int and Integer (this is called *autoboxing* and *autounboxing*) can lead to subtle bugs! You have to be aware what the compile-time types of your expressions are. Consider this:
```java
Map<String, Integer> a = new HashMap(), b = new HashMap();
a.put("c", 130); // put ints into the map
b.put("c", 130);
a.get("c") == b.get("c") // but what do we get out of the map?
```
## Summary
+ the abstraction function maps a concrete representation to the abstract value it represents
+ the rep invariant specifies legal values of the representation, and should be checked at runtime with `checkRep()`
+ equality should be an equivalence relation (reflexive, symmetric, transitive)
+ equality and hash code must be consistent with each other, so that data structures that use hash tables (like HashSet and HashMap) work properly
+ the abstraction function is the basis for equality in immutable data types
+ reference equality is the basis for equality in mutable data types; this is the only way to ensure consistency over time and avoid breaking rep invariants of hash tables
The topics of today's reading connect to our three properties of good software as follows:
+ **Safe from bugs.** Stating the rep invariant explicitly, and checking it at runtime with checkRep(), catches misunderstandings and bugs earlier, rather than continuing on with a corrupt data structure. Careful implementation of equality and hash codes avoids heinous bugs in collection data types like lists, sets, and maps.
+ **Easy to understand.** Rep invariants and abstraction functions explicate the meaning of a data type's representation, and how it relates to its abstraction.
+ **Ready for change.** Abstract data types separate the abstraction from the concrete representation, which makes it possible to change the representation without having to change client code.
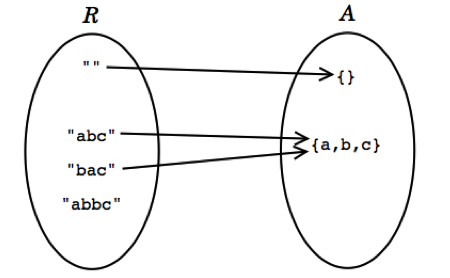Then the rep space R contains Strings, and the abstract space A is mathematical sets of characters. We can show the two value spaces graphically, with an arc from a rep value to the abstract value it represents. There are several things to note about this picture:
+ **Every abstract value is mapped to by some rep value**. The purpose of implementing the abstract type is to support operations on abstract values. Presumably, then, we will need to be able to create and manipulate all possible abstract values, and they must therefore be representable.
+ **Some abstract values are mapped to by more than one rep value**. This happens because the representation isn't a tight encoding. There's more than one way to represent an unordered set of characters as a string.
+ **Not all rep values are mapped**. In this case, the string "abbc" is not mapped. In this case, we have decided that the string should not contain duplicates. This will allow us to terminate the remove method when we hit the first instance of a particular character, since we know there can be at most one.
In practice, we can only illustrate a few elements of the two spaces and their relationships; the graph as a whole is infinite. So we describe it by giving two things:
1\. An *abstraction function* that maps rep values to the abstract values they represent:
> AF : R → A
The arcs in the diagram show the abstraction function. In the terminology of functions, the properties we discussed above can be expressed by saying that the function is surjective (also called *onto*), not necessarily bijective (also called *one-to-one*), and often partial.
2\. A *rep invariant* that maps rep values to booleans:
> RI : R → boolean
For a rep value r, RI(r) is true if and only if r is mapped by AF. In other words, RI tells us whether a given rep value is well-formed. Alternatively, you can think of RI as a set: it's the subset of rep values on which AF is defined.
Both the rep invariant and the abstraction function should be documented in the code, right next to the declaration of the rep itself:
```java
public class CharSet_NoRepeatsRep implements Set<Character> {
private String s;
// Rep invariant:
// s contains no repeated characters
// Abstraction Function:
// represents the set of characters found in s
...
}
```
A common confusion about abstraction functions and rep invariants is that they are determined by the choice of rep and abstract value spaces, or even by the abstract value space alone. If this were the case, they would be of little use, since they would be saying something redundant that's already available elsewhere.
The abstract value space alone doesn't determine AF or RI: there can be several representations for the same abstract type. A set of characters could equally be represented as a string, as above, or as a bit vector, with one bit for each possible character. Clearly we need two different abstraction functions to map these two different rep value spaces.
It's less obvious why the choice of both spaces doesn't determine AF and RI. The key point is that defining a type for the rep, and thus choosing the values for the space of rep values, does not determine which of the rep values will be deemed to be legal, and of those that are legal, how they will be interpreted. Rather than deciding, as we did above, that the strings have no duplicates, we could instead allow duplicates, but at the same time require that the characters be sorted, appearing in nondecreasing order. This would allow us to perform a binary search on the string and thus check membership in logarithmic rather than linear time. Same rep value space -- different rep invariant:
```java
public class CharSet_SortedRep implements Set<Character> {
private String s;
// Rep invariant:
// s[0] < s[1] < ... < s[s.length()-1]
// Abstraction Function:
// represents the set of characters found in s
...
}
```
Even with the same type for the rep value space and the same rep invariant RI, we might still interpret the rep differently, with different abstraction functions AF. Suppose RI admits any string of characters. Then we could define AF, as above, to interpret the array's elements as the elements of the set. But there's no *a priori* reason to let the rep decide the interpretation. Perhaps we'll interpret consecutive pairs of characters as subranges, so that the string "acgg" represents the set {a,b,c,g}.
```java
public class CharSet_SortedRangeRep implements Set<Character> {
private String s;
// Rep invariant:
// s.length is even
// s[0] <= s[1] <= ... <= s[s.length()-1]
// Abstraction Function:
// represents the union of the ranges
// {s[i]...s[i+1]} for each adjacent pair of characters
// in s
...
}
```
The essential point is that designing an abstract type means **not only choosing the two spaces** -- the abstract value space for the specification and the rep value space for the implementation -- **but also deciding what rep values to use and how to interpret them**.
It's critically important to write down these assumptions in your code, as we've done above, so that future programmers (and your future self) are aware of what the representation actually means. Why? What happens if different implementers disagree about the meaning of the rep?
mitx:b4aeda0673304efd839e6fab6d89ded3 AF and RI
### Example: Rational Numbers
Here's an example of an abstract data type for rational numbers. Look closely at its rep invariant and abstraction function.
```java
public class RatNum {
private final int numer;
private final int denom;
// Rep invariant:
// denom > 0
// numer/denom is in reduced form
// Abstraction Function:
// represents the rational number numer / denom
/** Make a new Ratnum == n. */
public RatNum(int n) {
numer = n;
denom = 1;
checkRep();
}
/**
* Make a new RatNum == (n / d).
* @param n numerator
* @param d denominator
* @throws ArithmeticException if d == 0
*/
public RatNum(int n, int d) throws ArithmeticException {
// reduce ratio to lowest terms
int g = gcd(n, d);
n = n / g;
d = d / g;
// make denominator positive
if (d < 0) {
numer = -n;
denom = -d;
} else {
numer = n;
denom = d;
}
checkRep();
}
}
```
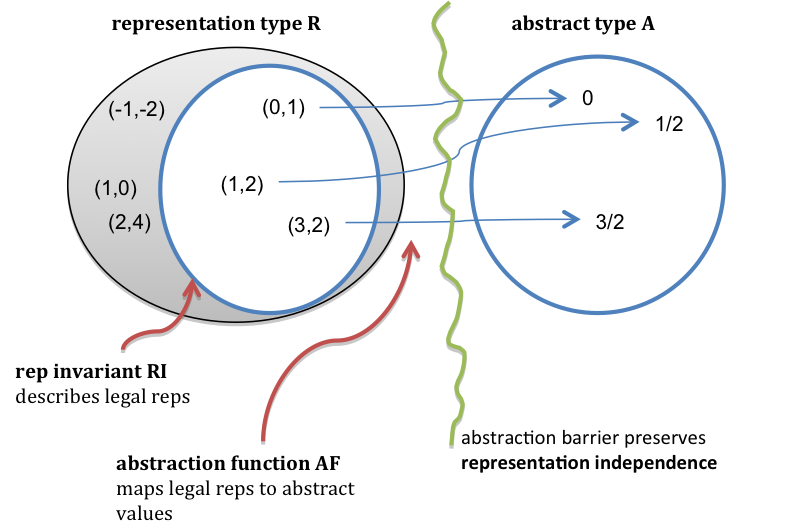Here is a picture of the abstraction function and rep invariant for this code. The RI requires that numerator/denominator pairs be in reduced form (i.e., lowest terms), so pairs like (2,4) and (18,12) above should be drawn as outside the RI.
It would be completely reasonable to design another implementation of this same ADT with a more permissive RI. With such a change, some operations might become more expensive to perform, and others cheaper.
### Checking the Rep Invariant
The rep invariant isn't just a neat mathematical idea. If your implementation asserts the rep invariant at run time, then you can catch bugs early. Here's a method for RatNum that tests its rep invariant:
```java
// Check that the rep invariant is true
// *** Warning: this does nothing unless you turn on assertion checking
// by passing -enableassertions to Java
private void checkRep() {
assert denom > 0;
assert gcd(numer, denom) == 1;
}
```
You should certainly call checkRep() to assert the rep invariant at the end of every operation that creates or mutates the rep -- in other words, creators, producers, and mutators. Look back at the RatNum code above, and you'll see that it calls checkRep() at the end of both constructors.
Observer methods don't normally need to call checkRep(), but it's good defensive practice to do so anyway. Why? Calling checkRep() in every method, including observers, means you'll be more likely to catch rep invariant violations caused by rep exposure.
Why is checkRep private? Who should be responsible for checking and enforcing a rep invariant -- clients, or the implementation itself?
### No Null Values in the Rep
Recall from the [specs reading](../06-specifications/specs) that null values are troublesome and unsafe, so much so that we try to remove them from our programming entirely.
In 6.005, the preconditions and postconditions of our methods implicitly require that objects and arrays be non-null.
We extend that prohibition to the reps of abstract data types. By default, in 6.005, the rep invariant implicitly includes `x != null` for every reference `x` in the rep that has object type (including references inside arrays or lists). So if your rep is:
```java
class CharSet {
String s;
}
```
then its rep invariant automatically includes `s != null`, and you don't need to state it in a rep invariant comment.
When it's time to implement that rep invariant in a checkRep() method, however, you still must *implement* the `s != null` check, and make sure that your checkRep() correctly fails when `s` is `null`. Often that check comes for free from Java, because checking other parts of your rep invariant will throw an exception if `s` is null. For example, if your checkRep() looks like this:
```java
private void checkRep() {
assert s.length() % 2 == 0;
...
}
```
then you don't need `assert s!= null`, because the call to `s.length()` will fail just as effectively on a null reference. But if `s` is not otherwise checked by your rep invariant, then assert `s != null` explicitly.
mitx:66dd1e7b3e854213992dde2cdd21a859 Checking the Rep Invariant
## Equality
Now we turn to how we define the notion of equality of values in a data type.
In the physical world, every object is distinct -- at some level, even two snowflakes are different, even if the distinction is just the position they occupy in space. (This isn't strictly true of all subatomic particles, actually, but true enough of large objects like snowflakes and baseballs and people.) So two physical objects are never truly "equal" to each other; they only have degrees of similarity.
In the world of human language, however, and in the world of mathematical concepts, you can have multiple names for the same thing. So it's natural to ask when two expressions represent the same thing: 1+2, √9, and 3 are alternative expressions for the same ideal mathematical value.
### Three Ways to Regard Equality
Formally, we can regard equality in several ways.
**Using an abstraction function**. Recall that an abstraction function f: R → A maps concrete instances of a data type to their corresponding abstract values. To use f as a definition for equality, we would say that a equals b if and only if f(a)=f(b).
**Using a relation**. An *equivalence* is a relation E ⊆ T x T that is:
+ reflexive: E(t,t) ∀ t ∈ T
+ symmetric: E(t,u) ⇒ E(u,t)
+ transitive: E(t,u) ∧ E(u,v) ⇒ E(t,v)
To use E as a definition for equality, we would say that a equals b if and only if E(a,b).
These two notions are equivalent. An equivalence relation induces an abstraction function (the relation partitions T, so f maps each element to its partition class). The relation induced by an abstraction function is an equivalence relation (check for yourself that the three properties hold).
A third way we can talk about the equality between abstract values is in terms of what an outsider (a client) can observe about them:
**Using observation**. We can say that two objects are equal when they cannot be distinguished by observation -- every operation we can apply produces the same result for both objects. Consider the set expressions {1,2} and {2,1}. Using the observer operations available for sets, cardinality |...| and membership ∈, these expressions are indistinguishable:
+ |{1,2}| = 2 and |{2,1}| = 2
+ 1 ∈ {1,2} is true, and 1 ∈ {2,1} is true
+ 2 ∈ {1,2} is true, and 2 ∈ {2,1} is true
+ 3 ∈ {1,2} is false, and 3 ∈ {2,1} is false
+ ... and so on
In terms of abstract data types, "observation" means calling operations on the objects. So two objects are equal if and only if they cannot be distinguished by calling any operations of the abstract data type.
### Example: Duration
Here's a simple example of an immutable ADT.
```java
public class Duration {
private final int mins;
private final int secs;
// rep invariant:
// mins >= 0, secs >= 0
// abstraction function:
// represents a span of time of mins minutes and secs seconds
/** Make a duration lasting for m minutes and s seconds. */
public Duration(int m, int s) {
mins = m; secs = s;
}
/** @return length of this duration in seconds */
public long getLength() {
return mins*60 + secs;
}
}
```
Now which of the following values should be considered equal?
```java
Duration d1 = new Duration (1, 2);
Duration d2 = new Duration (1, 3);
Duration d3 = new Duration (0, 62);
Duration d4 = new Duration (1, 2);
```
Think in terms of both the abstraction-function definition of equality, and the observational equality definition.
mitx:656052a10662494f87d5fd13d62a3abc Equality
### == vs. equals()
Like many languages, Java has two different operations for testing equality, with different semantics.
+ The == operator compares references. More precisely, it tests *referential* equality. Two references are == if they point to the same storage in memory. In terms of the snapshot diagrams we've been drawing, two references are == if their arrows point to the same object bubble.
+ The equals() operation compares object contents -- in other words, *object* equality, in the sense that we've been talking about in this reading. The equals operation has to be defined appropriately for every abstract data type.
For comparison, here are the equality operators in several languages: