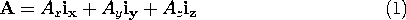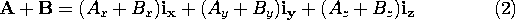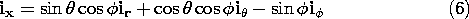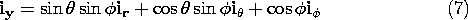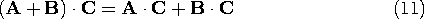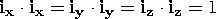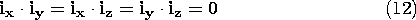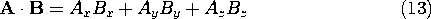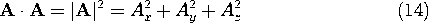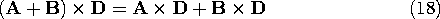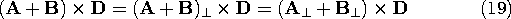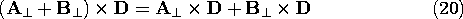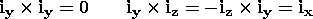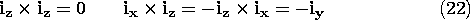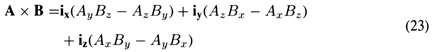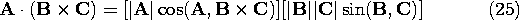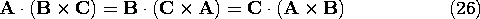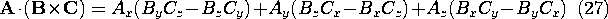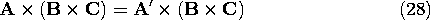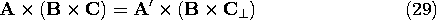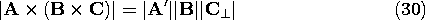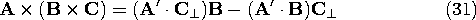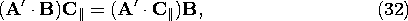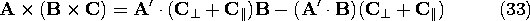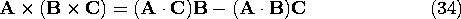1
Appendix: Vector Operations

Vectors

A vector is a quantity which possesses magnitude and direction. In order to describe a vector mathematically, a coordinate system having orthogonal axes is usually chosen. In this text, use is made of the Cartesian, circular cylindrical, and spherical coordinate systems. In these three-dimensional systems, any vector is completely described by three scalar quantities. For example, in Cartesian coordinates, a vector is described with reference to mutually orthogonal coordinate axes. Then the magnitude and orientation of the vector are described by specifying the three projections of the vector onto the three coordinate axes.

In representing a vector A mathematically, its direction along the three orthogonal coordinate axes must be given. The direction of each axis is represented by a unit vector i, that is, a vector of unit magnitude directed along the axis. In Cartesian coordinates, the three unit vectors are denoted i_x, i_y, i_z. In cylindrical coordinates, they are i_r, i , i_z, and in spherical coordinates, i_r, i , i. A, then, has three vector components, each component corresponding to the projection of A onto the three axes. Expressed in Cartesian coordinates, a vector is defined in terms of its components by

These components are shown in Fig. A.1.1.

Figure A.1.1 Vector A represented by its components in Cartesian coordiantes and unit vectors i.

Vector Addition

The sum of two vectors A = A_x i_x + A_y i_y + A_z i_z and B = B_x i_x + B_y i_y + B_z i_z is effected by adding the coefficients of each of the components, as shown in two dimensions in Fig. A.1.2a.

From (2), then, it should be clear that vector addition is both commutative, A + B = B + A, and associative, (A + B) + C = A + (B + C).

Figure A.1.2 (a) Graphical representation of vector addition in terms of specific coordinates. (b) Representation of vector addition independent of specific coordinates. Graphically, vector summation can be performed without regard to the coordinate system, as shown in Fig. A.1.2b, by noticing that the sum A + B is a vector directed along the diagonal of a parallelogram formed by A and B.

It should be noted that the representation of a vector in terms of its components is dependent on the coordinate system in which it is carried out. That is, changes of coordinate system will require an appropriate vector transformation. Further, the variables used must also be transformed. The transformation of variables and vectors from one coordinate system to another is illustrated by considering a transformation from Cartesian to spherical coordinates.

Example 1.2.1. Transformation of Variables and Vectors

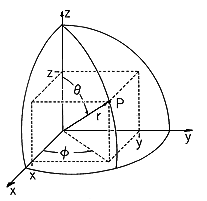
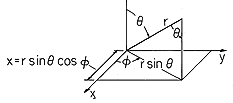
We are given variables in terms of x, y, and z and vectors such as A = A_x i_x + A_y i_y + A_z i_z. We wish to obtain variables in terms of r, , and and vectors expressed as A = A_r i_r + A i + A i. In Fig. A.1.3a, we see that the point P has two representations, one involving the variables x, y and z and the other, r, and . In particular, from Fig. 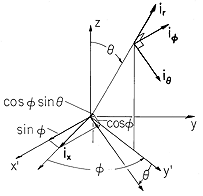A.1.3b, x is related to the spherical coordinates by Figure A.1.3 Specification of a point P in Cartesian and spherical coordinates. (b) Transformation from Cartesian coordinate x to spherical coordinates. (c) Transformation of unit vector in xdirection into spherical coordinates In a similar way, the variables y and z evaluated in spherical coordinates can be shown to be The vector A is transformed by resolving each of the unit vectors i_x, i_y, i_z in terms of the unit vectors in spherical coordinates. For example, i_x can first be resolved into components in the orthogonal coordinates (x^' , y^' , z) shown in Fig. A.1.3c. By definition, y^' is along the intersection of the = constant and the x-y planes. Also in the x - y plane is x^', which is perpendicular to the y^' - z plane. Thus, sin , cos , and 0 are the components of i_x along the x^' , y^', and z axes respectively. These components are in turn resolved into components along the spherical coordinate directions by recognizing that the component sin along the x^' axis is in the -i direction while the component of cos along the y^' axis resolves into components cos cos in the direction of i, and cos sin in the i_r direction. Thus, Similarly,

It must be emphasized that the concept of a vector is independent of the coordinate system. (In the same sense, in Chaps. 2 and 4, vector operations are defined independently of the coordinate system in which they are expressed.) A vector can be visualized as having the direction and magnitude of an arrow-tipped line element. This picture makes it possible to deal with vectors in a geometrical language that is independent of the choice of a particular coordinate system, one that will now be used to define the most important vector operations.

For analytical or numerical purposes, the operations are usually carried out in coordinate notation. Then, as illustrated, either in the text that follows or in the problems, each operation will be evaluated in a Cartesian coordinate system.

Definition of Scalar Product

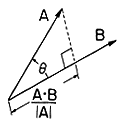
Given vectors A and B as illustrated in Fig. A.1.4, the scalar, or dot product, between the two vectors is defined as where is the angle between the two vectors.

Figure A.1.4 Illustration for definition of dot product. It follows directly from its definition that the scalar product is commutative. The scalar product is also distributive.

To see this, note that A C is the projection of A onto C times the magnitude of C, |C|, and B C is the projection of B onto C times |C|. Because projections are additive, (11) follows.

These two properties can be used to define the scalar product in terms of the vector components in Cartesian coordinates. According to the definition of the unit vectors,

With A and B expressed in terms of these components, it follows from the distributive and commutative properties that Thus, in agreement with (9), the square of the magnitude of a vector is

Definition of Vector Product

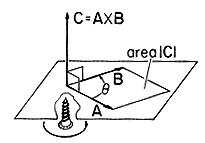
The cross-product of vectors A and B is a vector C having a magnitude and having a direction perpendicular to both A and B. Geometrically, the magnitude of C is the area of the parallelogram formed by the vectors A and B. The vector C has the direction of advance of a right-hand screw, as though driven by rotating A into B. Put another way, a right-handed coordinate system is formed by A - B - C, as is shown in Fig. A.1.5. The commonly accepted notation for the cross-product is

Figure A.1.5 Illustration for definition of vector-product It is useful to note that if the vector A is resolved into two mutually perpendicular vectors, A = A_\perp + A_\parallel, where A_\perp lies in the plane of A and B and is perpendicular to B and A_\parallel is parallel to B, then This equality follows from the fact that both cross-products have equal magnitude (since |A_\perp x B| = |A_\perp ||B| and |A|_\perp | = |A| sin ) and direction (perpendicular to both A and B).

The distributive property for the cross-product,

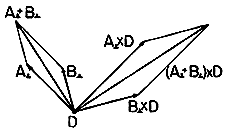
can be shown using (17) and the geometrical construction in Fig. A.1.6 as follows. First, note that (A + B)_\perp = (A_\perp + B_\perp ), where \perp denotes a component in the planes of A and D or B and D, respectively, and perpendicular to D. Thus, Figure A.1.6 Graphical representation showing that the vector-product is distributive. Now, we need only show that This equation is given graphical expression in Fig. A.1.6 by the vectors A_\perp , B_\perp, and their sum. To within a factor of |D|, the three vectors A_\perp x D, B_\perp x D, and their sum, are, respectively, the vectors A_\perp , B_\perp, and their sum, rotated by 90 degrees. Thus, the vector addition property already shown for A_\perp + B_\perp also applies to A_\perp x D + B_\perp x D.

Because interchanging the order of two vectors calls for a reassignment of the direction of the product vector (the direction of C in Fig. A.1.5), the commutative property does not hold. Rather,

Using the distributive law, the vector product of two vectors can be constructed in terms of their Cartesian coordinates by using the following properties of the vector products of the unit vectors.

Thus, A useful mnemonic for finding the cross-product in Cartesian coordinates is realized by noting that the right-hand side of (23) is the determinant of a matrix:

The Scalar Triple Product

The definition of the scalar triple product of vectors A, B, and C follows from Fig. A.1.7, and the definition of the scalar and vector products.

Figure A.1.7 Grpahical representation of scalar triple product. The scalar triple product is equal to the volume of the parallelepiped having the three vectors for its three bases. That is, in (25) the second term in square brackets is the area of the base parallelogram in Fig. A.1.7 while the first is the height of the parallelopiped. The scalar triple product is positive if the three vectors form a right-handed coordinate system in the order in which they are written; otherwise it is negative. Hence, a cyclic rearrangement in the order of the vectors leaves the value of the product unchanged.

It follows that the placing of the cross and the dot in a scalar triple product is arbitrary. The cross and dot can be interchanged without affecting the product.

Using the rules for evaluating the dot product and the cross-product in Cartesian coordinates, we have

The Double Cross-Product

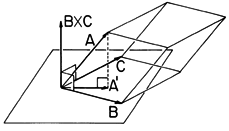
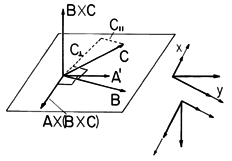
Consider the vector product A x (B x C). Is there another, sometimes more useful, way of expressing this double cross-product? Since the product B x C is perpendicular to the plane defined by B and C, then the final product A x (B x C) must lie in the plane of B and C. Hence, the vector product must be expressible as a linear combination of the vectors B and C. One way to find the coefficients of this linear combination is to evaluate the product in Cartesian coordinates. Here we prefer to use a geometric derivation.

Because the vector B x C is perpendicular to the plane defined by the vectors B and C, it follows from Fig. A.1.7 that

where A^' is the projection of A onto the plane defined by B and C. Next, we separate the vector C into a component parallel to B, C_\parallel, and a component perpendicular to B, C_\perp, as shown by Fig. A.1.8, so that Figure A.1.8 Graphical representation of double cross-product. Then, according to the properties of the cross-product, the magnitude of the vector product is given by and the direction of the vector product is orthogonal to A^' and lies in the plane defined by the vectors B and C, as shown in Fig. A.1.8 A rule for constructing a vector perpendicular to a given vector, A^', in an x - y plane is as follows. First, the two components of A^' with respect to any two orthogonal axes (x, y) are determined. Here these are the directions of C_\perp and B with components A^' C_\perp, and A^' \cdot B, respectively. Then, a new vector is constructed by interchanging the x and y components and changing the sign of one of them. According to this rule, Fig. A.1.8 shows that the vector A x (B x C) is given by Now, because C_\parallel has the same direction as B, and addition of (31) gives Now observe that A^' C = A \cdot C and A^' B = A \cdot B (which follow from the definition of A^' as the projection of A into the B - C plane), and the double cross-product becomes This result is particularly convenient because it does not contain any special notation or projections.

The vector identities found in this Appendix are summarized in Table III at the end of the text.