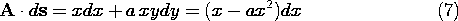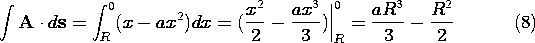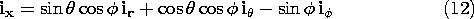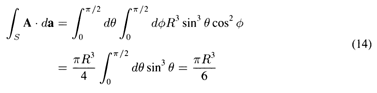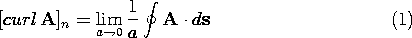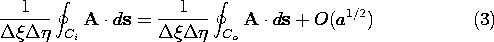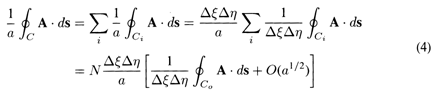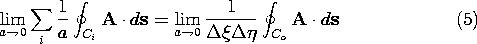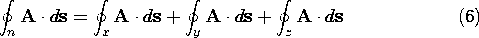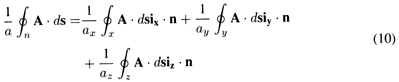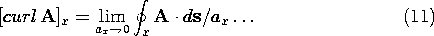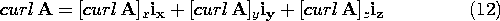2
Appendix: Line and Surface
Integrals and Proof that
Curl Results in a Vector

Line Integrals

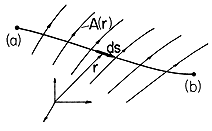
Consider a path connecting points (a) and (b) as shown in Fig. A.2.1. Assume that a vector field A(r) exists in the space in which the path is situated. Then the line integral of A(r) is defined by To interpret (1), think of the path between (a) and (b) as subdivided into differential vector segments ds. At every vector segment, the vector A(r) is evaluated and the dot product is formed. The line integral is then defined as the sum of these dot products in the limit as ds approaches zero. A line integral over a path that closes on itself is denoted by the symbol A ds.

Figure A.2.1 Configuration for integration of vector field A along line having differential length ds between points (a) and (b). To perform a line integration, the integral must first be reduced to a form that can be evaluated using the rules of integral calculus. This is done with the aid of a coordinate system. The following example illustrates this process.

Example 2.1.1. Line Integral

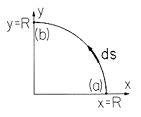
Given the two-dimensional vector field find the line integral along a quarter circle of radius R as shown in Fig. A.2.2.

Figure A.2.2 Integration line having shape of quarter segment of a circle with radius R and differential element ds. Using a Cartesian coordinate system, the differential line segment ds has the components dx and dy.

Now x and y are not independent but are constrained by the fact that the integration path follows a circle defined by the equation Differentiation of (4) gives and therefore Thus, the dot product A ds can be written as a function of the variable x alone.

When the path is described in the sense shown in Fig. A.2.4, x decreases from R to zero. Therefore, If the path is not expressible in terms of an analytic function, the evaluation of the line integral becomes difficult. If everything else fails, numerical methods can be employed.

Surface Integrals

Given a vector field A(r) in a region of space containing a specified (open or closed) surface S, an important form of the surface integral of A over S is The vector da has a magnitude that represents the differential area of a surface element and a direction that is normal to that area. To interpret (9), think of the surface S as subdivided into these differential area elements da. At each area element, the differential scalar A da is evaluated and the surface integral is defined as the sum of these dot products over S in the limit as da approaches zero. The surface integral _S A da is also called the ``flux" of the vector A through the surface S.

To evaluate a surface integral, a coordinate system is introduced in which the integration can be performed according to the methods of integral calculus. Then the surface integral is transformed into a double integral in two independent variables. This is best illustrated with the aid of a specific example.

Example 2.2.2. Surface Integral

Given the vector field find the surface integral \int_S A da, where S is one eighth of a spherical surface of radius R in the first octant of a sphere (0 \leq /2, 0 \leq \leq /2). Because the surface lies on a sphere, it is best to carry out the integration in spherical coordinates. To transform coordinates from Cartesian to spherical, recall from (A.1.3) that the x coordinate is related to r, , and by and from (A.1.6), the unit vector i_x is Therefore, because the area element da is the surface integral becomes

A surface integral of a vector A over a closed surface is indicated by Note also that we use a single integral sign for a surface integral, even though, in fact, two integrations are involved when the integral is actually evaluated in terms of a coordinate system.

2.2 Proof that the Curl Operation Results in aVector

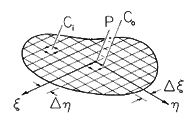
The definition assigns a scalar, [curl A]_n, to each direction n at the point P under consideration. The limit must be independent of the shape of the contour C (as long as all its points approach the point P in the limit as the area a of the contour goes to zero). The identification of curl A as a vector also implies a proper dependence of this limit upon the orientation of the normal n of a. The purpose of this appendix is to show that these two requirements are indeed satisfied by (1). We shall prove the following facts:

by its normal vector n, the quantity on the right in (1) is independent of the shape of the contour. (The notation [curl A]_n, is introduced at this stage only as a convenient abbreviation for the expression on the right.) \item 2. If [curl A]_n is indeed the component of a vector [curl A] in the n direction and n is a unit normal in the n direction, then

where [curl A] is a vector defined at the point (x, y, z).

The proof of (1) follows from the fact that any closed contour integral can be built up from a superposition of contour integrals around a large number of rectangular contours C_i, as shown in Fig. A.2.3. All rectangles have sides , \Delta. If the entire contour containing the rectangles is small (a 0), then the contour integral around each rectangle differs from that for the contour C_o at the origin only by a term on the order of the linear dimension of the contour, a^1/2, times the area . 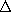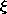This is true provided that the distance from the origin to any point on the contour does not exceed a^1/2 by an order of magnitude and that A is once differentiable in the neighborhood of the origin. We have

Figure A.2.3 Separation of closed contour integral into large number of integrals over rectangular contours. Therefore, where N is the number of rectangles into which the contour C has been subdivided. However, N = a/( 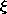), and therefore we find The expression on the left refers to the original contour, while the expression on the right refers to the rectangular contour at the origin. Since a contour of arbitrary shape can be constructed by a proper arrangement of rectangular contours, we have proven that the expression \lim_{a 0} \int A ds /a is independent of the shape of the contour as long as (3) holds.

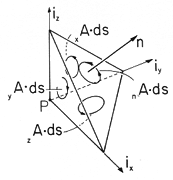
Turning to the proof that (1) defines the component of a vector, we recognize that the shape of the contour is arbitrary when evaluating \int A ds /a. We displace the plane in which the contour lies by a differential amount away from the point P(x, y, z), as shown in Fig. A.2.4 which does not affect the value of [curl A]_n as defined in (1). The intersection of the plane with the three coordinate planes through P is a triangle. We pick the triangle for the contour C in (1).

Figure A.2.4 Arbitrary incremental contour integral having normal n analyzed into integration contours enclosing surface, having normals in the directions of the Cartesian coordinates. It follows from Fig. A.2.4 that the contour integral around the triangular contour in the plane perpendicular to n can also be written as the sum of three integrals around the three triangular contours in the respective coordinate planes. Indeed, each of the added sections of line are traversed in one contour integration in the opposite direction, so that the integrals over the added sections of the line cancel upon summation and we have where each contour integral is denoted by the subscript taken from the unit vector normal to the plane of the contour.

We further note that the areas a_x, a_y, a_z of the three triangles in the respective coordinate planes are the projections of the area a onto the corresponding coordinate plane.

Thus, by dividing (6) by a and making use of (7), (8), and (9), we have: Now, since the contours are already taken around differential area elements, the limit a 0 is already implied in (10). Thus, we have the quantities But (10) is the definition of the component in the n direction of a vector: It is therefore legitimate to define at every point x, y, z in space a vector quantity, curl A, whose x-, y-, and z-components are evaluated as the limiting expressions of (1).