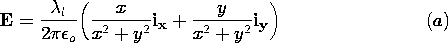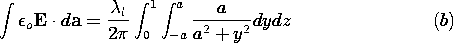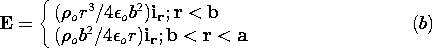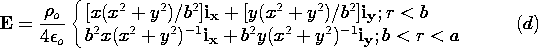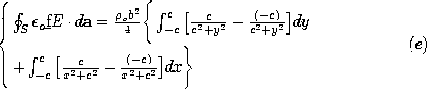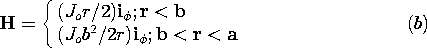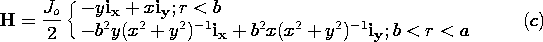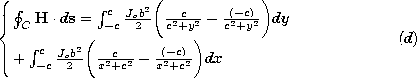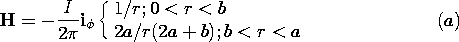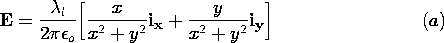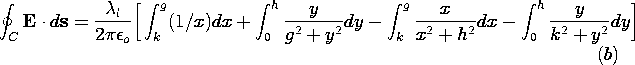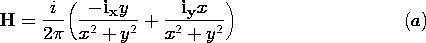The Lorentz Law in Free Space* | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.1.1* | Assuming in Example 1.1.1 that vi = 0
and that Ex < 0, show that
by the time the electron has reached the position x = h, its
velocity is 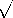 -2eExh/m. In an electric field of only Ex =
1v/cm = 10-2 v/m, show that by the time it reaches h =
10-2 m, the electron has reached a velocity of 5.9 x 103
m/s. -2eExh/m. In an electric field of only Ex =
1v/cm = 10-2 v/m, show that by the time it reaches h =
10-2 m, the electron has reached a velocity of 5.9 x 103
m/s.
| ||||||||||
| 1.1.2 | An electron moves in vacuum under the same conditions as in Example
1.1.1 except that the electric field takes the form E = Ex ix +
Ey iy where Ex and Ey are given constants. When t = 0, the
electron is at 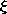 x = 0 and x = 0 and 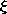 y = 0 and the velocity d y = 0 and the velocity d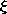 x /dt
= vi and d x /dt
= vi and d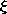 y /dt = 0. y /dt = 0.
| ||||||||||
| 1.1.3* | An electron, having velocity v = vi iz, experiences the field
H = Ho iy and E = Eo ix, where Ho and Eo are
constants. Show that the electron retains this velocity if Eo =
vi 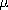 o Ho. o Ho.
| ||||||||||
| 1.1.4 | An electron has the initial position x = 0, y = 0, z = zo.
It has an initial velocity v = vo ix and moves in the uniform
and constant fields E = Eo iy, H = Ho iy.
direction,
| ||||||||||
Charge and Current Densities | |||||||||||
| 1.2.1* | The charge
density is 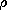 o r/R coulomb/m3 throughout the volume of a
spherical region having radius R, with o r/R coulomb/m3 throughout the volume of a
spherical region having radius R, with 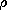 o a constant and r
the distance from the center of the region (the radial coordinate in
spherical coordinates). Show that the total charge
associated with this charge density is q = o a constant and r
the distance from the center of the region (the radial coordinate in
spherical coordinates). Show that the total charge
associated with this charge density is q =  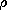 o R3 coulomb. o R3 coulomb.
| ||||||||||
| 1.2.2 | In terms of given constants 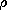 o and a, the net charge density
is o and a, the net charge density
is 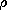 = ( = (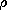 o /a2) (x2 + y2 + z2) coulomb/m3.
What is the total charge q (coulomb) in the cubical region -a < x
< a, -a < y < a, -a < z < a? o /a2) (x2 + y2 + z2) coulomb/m3.
What is the total charge q (coulomb) in the cubical region -a < x
< a, -a < y < a, -a < z < a?
| ||||||||||
| 1.2.3* | With Jo and a given constants, the current density is J =
(Jo/a2)(y2 + z2) [ix + iy + iz ]. Show that the total
current i passing through the surface x = 0, -a < y < a, -a
< z < a is i = 8Jo a2/3 amp.
| ||||||||||
| 1.2.4 | In cylindrical coordinates (r, 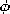 , z) the current density is
given in terms of constants Jo and a by J = Jo (r/a)2
iz (amp/m2). What is the net current i (amp) through the
surface z = 0, r < a? , z) the current density is
given in terms of constants Jo and a by J = Jo (r/a)2
iz (amp/m2). What is the net current i (amp) through the
surface z = 0, r < a?
| ||||||||||
| 1.2.5* | In cylindrical coordinates, the electric field in the annular region
b < r < a is E = ir Eo (b/r), where Eo is a given
negative constant.
When t = 0, an electron having mass m and charge q = -e has no
velocity and is positioned at r = 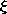 r = b. r = b.
| ||||||||||
Gauss' Integral Law | |||||||||||
| 1.3.1* | Consider how Gauss' integral law, (1), is evaluated for a surface
that is not naturally symmetric. The charge distribution is the
uniform line charge of Fig. 1.3.7 and hence E is given by (13).
However, the surface integral on the left in (1) is to be evaluated
using a surface that has unit length in the z direction and a square
cross-section centered on the z axis. That is, the surface is
composed of the planes z = 0, z = 1, x =  a, and y = a, and y =  a. Thus, we know from evaluation of the right-hand side of (1) that
evaluation of the surface integral on the left should give the line
charge density
a. Thus, we know from evaluation of the right-hand side of (1) that
evaluation of the surface integral on the left should give the line
charge density 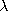 l. l.
| ||||||||||
| 1.3.2 | Using the spherical symmetry and a spherical surface, the electric
field associated with the point charge q of Fig. 1.3.6 is found to be
given by (12). Evaluation of the left-hand side of (1) over any other
surface that encloses the point charge must also give q. Suppose that
the closed surface S is composed of a hemisphere of radius a in the upper
half-plane, a hemisphere of radius b in the lower half-plane, and a
washer-shaped flat surface that joins the two. In spherical
coordinates (defined in Table I), these three parts of the closed
surface S are defined by (r = a, 0 < 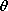 < < 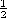  ,
0 ,
0  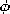 < 2 < 2 ), (r = b, ), (r = b, 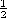  < < 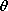 < <  , 0 , 0
 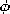 < 2 < 2 ), and ( ), and (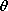 = = 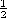  , b , b  r \leq
a, 0 r \leq
a, 0  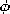 < 2 < 2 ). For this surface, use (12) to evaluate
the left-hand side of (1) and show that it results in q. ). For this surface, use (12) to evaluate
the left-hand side of (1) and show that it results in q.
| ||||||||||
| 1.3.3* | A cylindrically symmetric charge configuration
extends to infinity in the  z directions and has the same
cross-section in any constant z plane. Inside the radius b, the
charge density has a parabolic dependence on radius while over the range
b < r < a outside that radius, the charge density is zero. z directions and has the same
cross-section in any constant z plane. Inside the radius b, the
charge density has a parabolic dependence on radius while over the range
b < r < a outside that radius, the charge density is zero.

| ||||||||||
| 1.3.4 | In a spherically symmetric configuration, the region r < b has the
uniform charge density 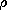 b and is surrounded by a region b < r <
a having the uniform charge density b and is surrounded by a region b < r <
a having the uniform charge density 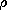 a. At r = b there is no
surface charge density, while at r = a there is that surface charge
density that assures E = 0 for a < r. a. At r = b there is no
surface charge density, while at r = a there is that surface charge
density that assures E = 0 for a < r.
| ||||||||||
| 1.3.5* | The region between the plane parallel sheets of surface charge
density shown in Fig. 1.3.8 is filled with a charge density 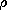 =
2 =
2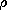 o z/s, where o z/s, where  o is a given constant. Again,
assume that the electric field below the lower sheet is Eo iz and
show that between the sheets o is a given constant. Again,
assume that the electric field below the lower sheet is Eo iz and
show that between the sheets
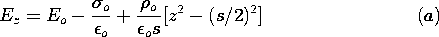 | ||||||||||
| 1.3.6 | In a configuration much like that of Fig. 1.3.8, there are three
rather than two sheets of charge. One, in the plane z = 0, has the
given surface charge density  o. The second and third,
respectively located at z = s/2 and z = -s/2, have unknown charge
densities o. The second and third,
respectively located at z = s/2 and z = -s/2, have unknown charge
densities  a and a and  b. The electric field outside the
region - b. The electric field outside the
region -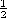 s < z < s < z < 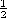 s is zero, and s is zero, and  a =
2 a =
2 b. Determine b. Determine  a and a and  b. b.
| ||||||||||
| 1.3.7 | Particles having charges of the same sign are constrained in their
positions by a plastic tube which is tilted with respect to the
horizontal by the angle  , as shown in Fig. P1.3.7. Given that
the lower particle has charge Qo and is fixed, while the upper one
(which has charge Q and mass M) is free to move without friction, at
what relative position, , as shown in Fig. P1.3.7. Given that
the lower particle has charge Qo and is fixed, while the upper one
(which has charge Q and mass M) is free to move without friction, at
what relative position, 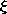 , can the upper particle be in a state of
static equilibrium? , can the upper particle be in a state of
static equilibrium?
 | ||||||||||
Ampère's Integral Law | |||||||||||
| 1.4.1* | A static H field is produced by the cylindrically symmetric current
density distribution J = Jo \exp (-r/a) iz, where Jo and a
are constants and r is the radial cylindrical coordinate. Use the
integral form of Ampère's law to show that
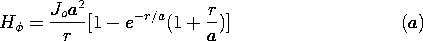 | ||||||||||
| 1.4.2* | In polar coordinates, a uniform current density Jo iz
exists over the cross-section of a wire having radius b. This current
is returned in the -z direction as a uniform surface current at the
radius r = a > b.
| ||||||||||
| 1.4.3 | In a configuration having axial symmetry about the z axis and
extending to infinity in the  z directions, a line current I
flows in the -z direction along the z axis. This current is returned
uniformly in the +z direction in the region b < r < a. There is no
current density in the region 0 < r < b and there are no surface current
densities. z directions, a line current I
flows in the -z direction along the z axis. This current is returned
uniformly in the +z direction in the region b < r < a. There is no
current density in the region 0 < r < b and there are no surface current
densities.
| ||||||||||
| 1.4.4* | In a configuration having axial symmetry about the z axis, a line
current I flows in the -z direction along the z axis. This current is
returned at the radii a and b, where there are uniform surface current
densities Kza and Kzb, respectively. The current density is
zero in the regions 0 < r < b, b < r < a and a < r.
| ||||||||||
| 1.4.5 | Uniform surface current densities K =  Ko iy are in the
planes z = Ko iy are in the
planes z =   s, respectively. In the region - s, respectively. In the region -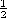 s < z < s < z < 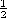 s, the current density is J = 2Jo z/siy.
In the region z < - s, the current density is J = 2Jo z/siy.
In the region z < - 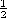 s, H = 0. Determine H for
- s, H = 0. Determine H for
-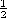 s < z. s < z.
| ||||||||||
Charge Conservation in Integral Form | |||||||||||
| 1.5.1* | In the region of space of interest, the charge density is uniform
and a given function of time, 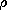 = = 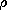 o (t).
Given that the
system has spherical symmetry, with r the distance from the center of
symmetry, use the integral form of the law of charge conservation to
show that the current density is o (t).
Given that the
system has spherical symmetry, with r the distance from the center of
symmetry, use the integral form of the law of charge conservation to
show that the current density is
 | ||||||||||
| 1.5.2 | In the region x > 0, the charge density is known to be uniform and the
given function of time 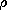 = = 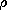 o (t). In the plane x = 0, the
current density is zero. Given that it is x directed and only
dependent on x and t, what is J? o (t). In the plane x = 0, the
current density is zero. Given that it is x directed and only
dependent on x and t, what is J?
| ||||||||||
| 1.5.3* | In the region z > 0, the current density J = 0. In the region
z < 0, J = Jo(x, y) cos 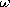 t iz, where Jo is a given
function of (x, y). Given that when t = 0, the surface charge density t iz, where Jo is a given
function of (x, y). Given that when t = 0, the surface charge density
 s = 0 over the plane z = 0, show that for t > 0, the
surface charge density in the plane z = 0 is s = 0 over the plane z = 0, show that for t > 0, the
surface charge density in the plane z = 0 is  s (x, y, t) =
[Jo (x, y)/ s (x, y, t) =
[Jo (x, y)/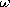 ] sin ] sin 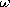 t. t.
| ||||||||||
| 1.5.4 | In cylindrical coordinates, the current density J = 0 for r < R,
and J = Jo (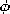 , z) sin , z) sin 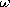 tir for r > R. The surface
charge density on the surface at r = R is tir for r > R. The surface
charge density on the surface at r = R is  s ( s (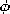 , z, t) =
0 when t = 0. What is , z, t) =
0 when t = 0. What is  s ( s (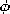 , z, t) for t > 0? , z, t) for t > 0?
| ||||||||||
Faraday's Integral Law | |||||||||||
| 1.6.1* | Consider the calculation of the circulation of E, the left-hand
side of (1), around a contour consisting of three segments enclosing
a surface lying in the x - y plane: from (x, y) = (0, 0)
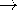 (g, s) along the line y = sx/g; from (x, y) = (g, s) (g, s) along the line y = sx/g; from (x, y) = (g, s)
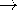 (0, s) along y = s and from (x, y) = (0, s)
to (0, 0) along x = 0. (0, s) along y = s and from (x, y) = (0, s)
to (0, 0) along x = 0.
| ||||||||||
| 1.6.2 | The situation is the same as in Prob. 1.6.1 except that the first
segment of the closed contour is along the curve y = s(x/g)2.
| ||||||||||
| 1.6.3* | The E field of a line charge density uniformly distributed
along the z axis is given in cylindrical coordinates by (1.3.13).
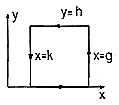
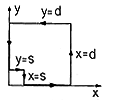 | ||||||||||
| 1.6.4 | A closed contour consisting of six segments is shown in Fig. P1.6.4.
For the electric field intensity of Prob. 1.6.3, calculate
the line integral of E  ds on each of these segments and
show that the integral around the closed contour is zero. ds on each of these segments and
show that the integral around the closed contour is zero.
| ||||||||||
| 1.6.5* | The experiment in Fig. 1.6.4 is carried out with the coil
positioned horizontally, as shown in Fig. 1.7.2. The left
edge of the coil is directly below the wire, at a distance d, while
the right edge is at the radial distance R from the wire, as shown.
The area element da is y directed (the vertical direction).
| ||||||||||
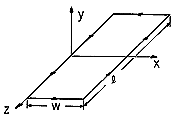
| 1.6.6 | The magnetic field intensity is given to be H = Ho(t) (ix + iy
), where Ho(t) is a given
function of time. What is the circulation of E around the contour
shown in Fig. P1.6.6?
 | ||||||||||
| 1.6.7* | In the plane y = 0, there is a uniform surface charge density
 s = s =  o. In the region y < 0, E = E1 ix + E2
iy where E1 and E2 are
given constants. Use the continuity conditions of Gauss and Faraday,
(1.3.17) and (12), to show that just above the plane y = 0,
where y = 0+, the electric field intensity is E = E1 ix + [E2
+ ( o. In the region y < 0, E = E1 ix + E2
iy where E1 and E2 are
given constants. Use the continuity conditions of Gauss and Faraday,
(1.3.17) and (12), to show that just above the plane y = 0,
where y = 0+, the electric field intensity is E = E1 ix + [E2
+ ( o / o / o)]iy. o)]iy.
| ||||||||||
| 1.6.8 | Inside a circular cylindrical region having radius r = R, the
electric field intensity is E = Eo iy, where Eo is a
given constant. There is a surface charge density  o cos o cos
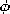 on the surface at r = R (the polar coordinate on the surface at r = R (the polar coordinate 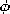 is
measured relative to the x axis). What is E just
outside the surface, where r = R+? is
measured relative to the x axis). What is E just
outside the surface, where r = R+?
| ||||||||||
Integral Magnetic Flux Continuity Law | |||||||||||
| 1.7.1* | A region is filled by a uniform magnetic field intensity Ho(t)iz.
| ||||||||||
| 1.7.2 | With Ho(t) a given function of time and d a given constant,
three distributions of H are proposed.
   | ||||||||||
| 1.7.3* | In the plane y = 0, there is a given surface current density K = Ko ix. In the region y < 0, H = H1 iy + H2 iz. Use the continuity conditions of (1.4.16) and (6) to show that just above the current sheet, where y = 0+, H = (H1 - Ko)iy + Hz iz. | ||||||||||
| 1.7.4 | In the circular cylindrical surface r = R, there is a surface current density K = Ko iz. Just inside this surface, where r = R, H = H1 ir. What is H just outside the surface, where r = R+? |